Propagation du Son

But de la manipulation

• Etude de la propagation du son comme une onde longitudinale de pression
• Expérience de création d'ondes stationnaires

Eléments théoriques

Equation d'Onde

De manière générale, on peut décrire le cas d'une onde qui se propage dans une seule direction (par exemple une colonne d'air) avec l'équation d'onde comme:

$$\frac{\partial^2}{\partial z^2}\mathcal{f}(z, t) - \frac{1}{v}\frac{\partial^2}{\partial t^2}\mathcal{f}(z, t) = 0$$

où $v$ est la vitesse de l'onde. Cette équation admet une infinité de solutions du type:

$$\mathcal{f}(z, t) = A \mathcal{f_-} (v t - z) + B \mathcal{f}_+ (v t + z)$$

où les constantes $A$ et $B$ sont arbitraires (également que des fonctions $\mathcal{f}_\pm$).

La chose intéressante est l'aspect général de cette solution. Toute fonction qui a comme argument $(vt -z)$ ou $(vt+z)$ est une solution de l'équation d'onde !

On voit que chacune des fonctions $\mathcal{f}_\pm$ décrit la propagation d'une onde car la valeur de la fonction a une coordonnée $(z_0, t_0=0)$ qui est la même que pour un temps $t$ en un emplacement $z = z_0 \pm v t$.

Question: Prouvez que la fonction $ \mathcal{f_-} (v t - z) $ est une onde et a la même valeur aux coordonnées $(z_0, t_0=0)$ qu'aux coordonnées $(z = z_0 + v t, t)$.

En fait, on peut voir que la fonction $\mathcal{f}_-(v t - z)$ décrit une onde que se déplace vers les $z$ croissants, et $\mathcal{f}_+(v t + z)$ une onde se déplaçant en sens inverse ($z$ décroissants).

Réflections et ondes stationnaires

Quand le milieu dans lequel les ondes se déplacent est fini (par exemple une corde finie pour les ondes longitudinales ou un tube d'air d'une taille donnée pour les ondes transversales sonores), si par exemple l'onde originale, $\mathcal{f}_-(v t - z)$, voyage vers les $z$ positifs, elle sera réfléchie à la fin et va devenir une onde $\mathcal{f}_+(v t + z)$. La manière dont une onde est réfléchie va dépendre des conditions sur l'extrémité de la corde ou de la colonne d'air.

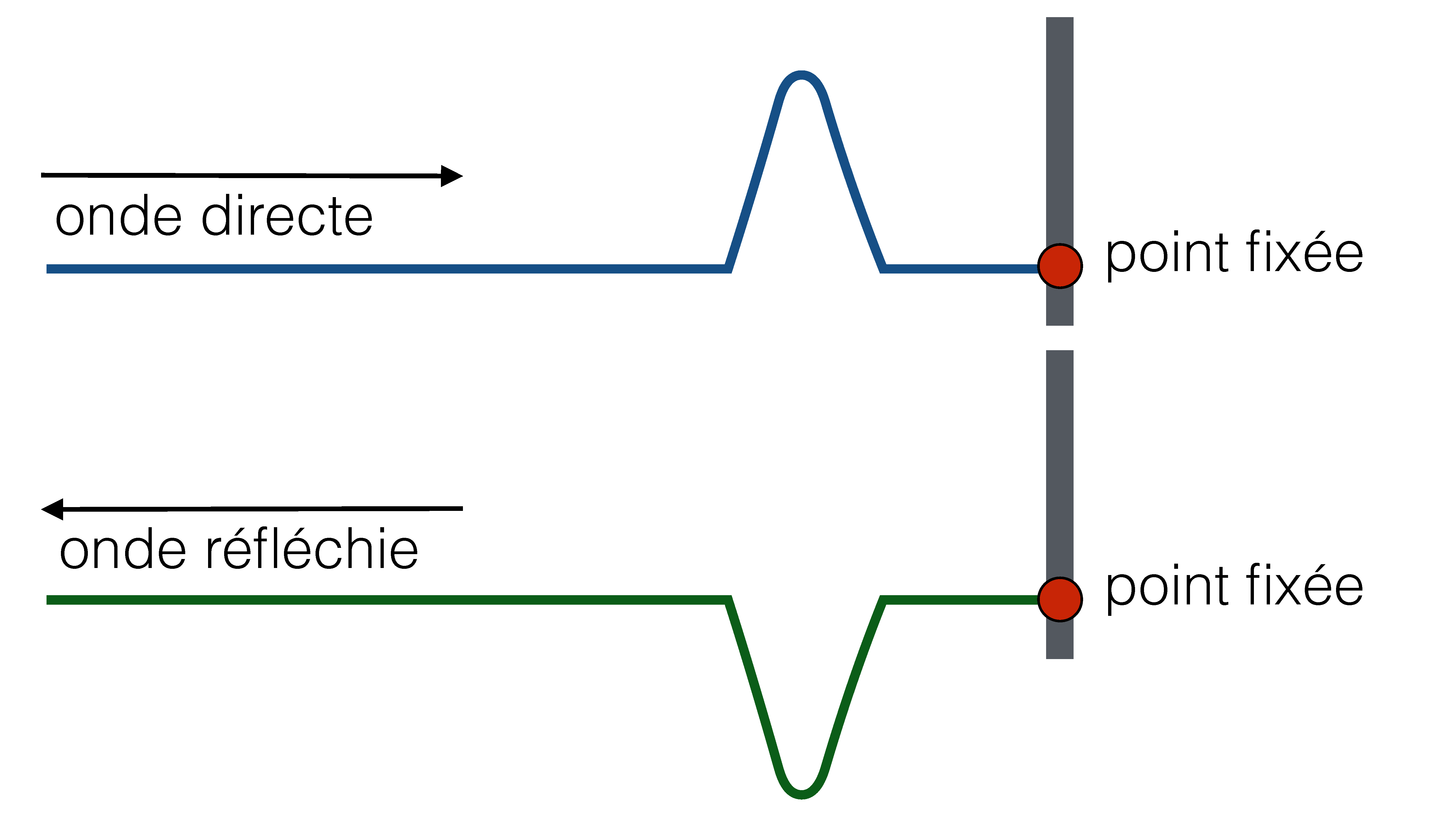
Par exemple, on peut imaginer une onde (avec déplacement vertical) qui se déplace vers la droite le long d'une corde dont l'extrémité est fixée ou pincée. Lorsque les ondes approchent la fin fixée, les forces internes de restauration qui autorisent l'onde à se propager vont exercer une force vers le haut à la fin de la corde. Mais, puisque la fin est pincée, elle ne peut bouger. En accord avec la 3e loi de Newton, le mur va excercer une force vers le bas égale et opposée sur le bout de la corde. Cette nouvelle force crée une onde qui se propage de la droite vers la gauche en sens inverse, avec la même vitesse et amplitude que l'onde incidente, mais avec une amplitude opposée (voir la figure ci-dessous).

Une onde sur une corde se réfléchissant sur une extrémité fixée. L'onde réfléchie (en vert) subit un changement d'amplitude

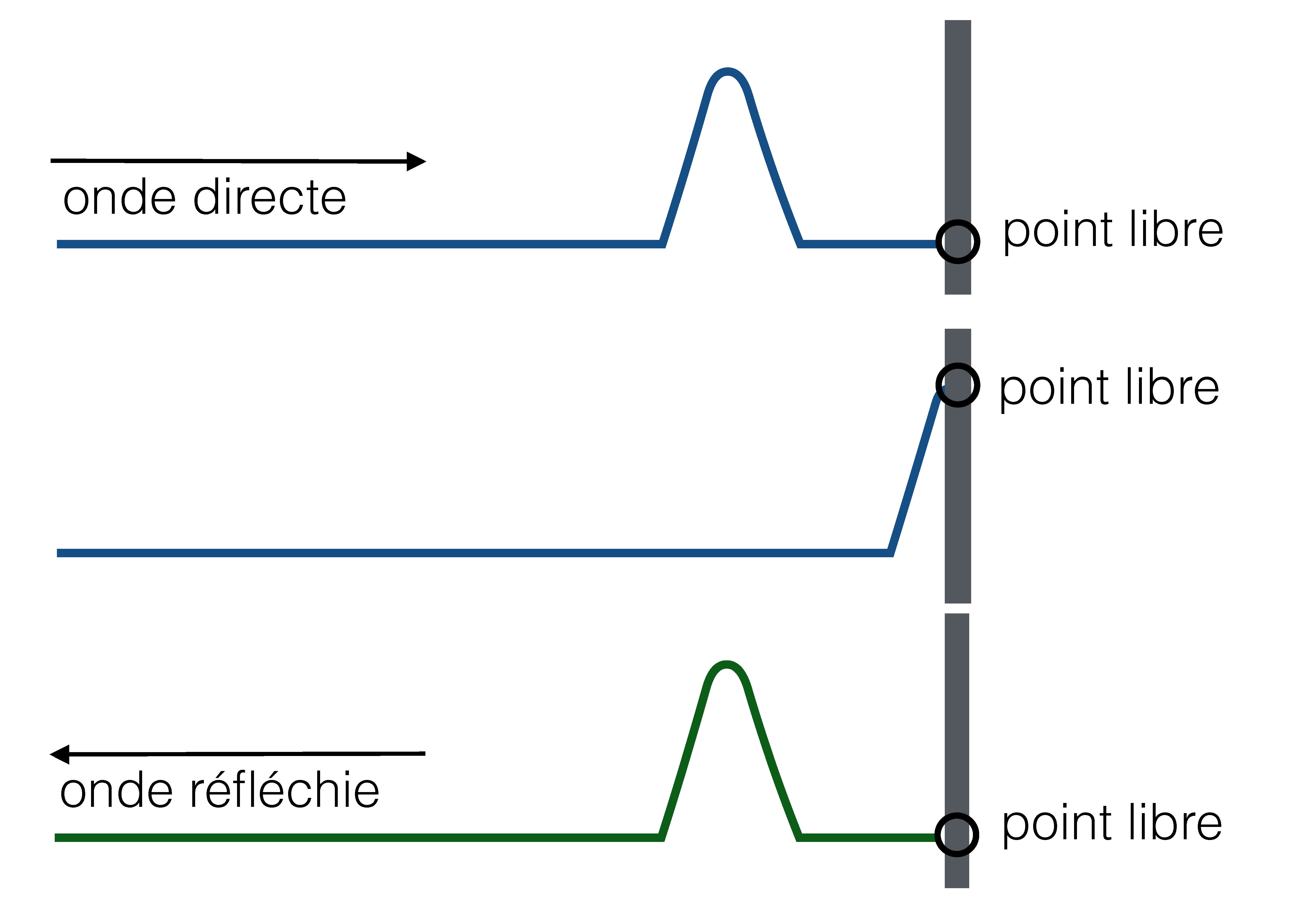
D'un autre coté, si l'extrémité est autorisée à se déplacer librement verticalement, alors les forces verticales finales sont nulles et l'onde réfléchie va se propager vers l'arrière mais cette fois avec la même amplitude que l'onde originale.

Une onde sur une corde se réfléchissant sur une extrémité *libre*. L'onde réfléchie (en vert) se propage avec la même amplitude.

Si nous prenons maintenant par exemple une onde cosinusoïdale avec vitesse $v =\frac{\omega}{k}$:

$$\mathcal{f}_-(vt - z) = \cos (\omega t - k z) = \cos \left[\omega\left( t - \frac{k}{\omega}z\right)\right] = \cos \left[\omega\left( t - \frac{z}{v}\right)\right]$$

L'onde réfléchie aura nécessairement aussi la forme d'une onde sinusoïdale, de même fréquence $\nu = \omega/2\pi$, et de même amplitude, mais se dirigeant en sens opposé et avec un déphasage dans le temps, $\phi$:

$$\mathcal{f}_+(vt + z) = \cos \left[\omega \left(t + \frac{z}{v}\right) + \phi\right]$$

Si l'une des extrémité de la corde ($z =0$) est fixée alors $\phi = \pi$, et si l'extrémité (en $z =0$) est libre, alors $\phi =0$. La combinaison des deux ondes, l'incidente et la réfléchie, va être donnée par:

$$\mathcal{f}(z,t) = \cos\left[\omega\left(t - \frac{z}{v}\right)\right] + \cos\left[\omega\left(t + \frac{z}{v}\right) + \phi\right]$$

Un peu de trigonométrie nous donne:

$$\mathcal{f}(z,t) = 2\cdot\cos\left[\frac{\omega\left(t - \frac{z}{v}\right)+\omega\left(t + \frac{z}{v}\right) + \phi}{2} \right]\cdot \cos\left[\frac{\omega\left(t - \frac{z}{v}\right)-\omega\left(t + \frac{z}{v}\right) - \phi}{2} \right]$$

$$\mathcal{f}(z,t) = 2\cdot\cos\left(\omega t +\frac{\phi}{2}\right)\cdot\cos\left(\omega \frac{z}{v} +\frac{\phi}{2}\right)$$

Ce qui est l'équation d'une onde stationnaire.

La suite est un morceau de code en python montrant une onde stationnaire (en noir) formée par deux ondes cosinusoïdales se déplacant dans des directions opposées (l'étudiant est invité à vérifier la version online de ces notes pour voir l'animation).

%matplotlib inline
import seaborn as sb
sb.set_context("poster")
sb.set_style("dark")
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import animation
from JSAnimation import IPython_display

fig = plt.figure()
ax = plt.axes(xlim=(0, 30), ylim=(-3, 3))
line1, = ax.plot([], [], lw=2, color="cyan")
line2, = ax.plot([], [], lw=2, color="red")
line3, = ax.plot([], [], lw=2, color="black")
plt.grid()

def animate(i):
    x = np.linspace(0, 30, 1000)
    c = np.cos(x + i * 0.02 * np.pi)
    s = np.sin(x - i * 0.02 * np.pi)
    line1.set_data(x, c)
    line2.set_data(x, s)
    line3.set_data(x, c+s)

    return line1, line2, line3,

animation.FuncAnimation(fig, animate,
                        frames=100, interval=30)

– +

Once Loop Reflect

Noeud et Antinoeuds

On appelle noeud cette position d'ondes stationnaires où l'onde s'annule à tout moment. Par contre, les positions où l'onde atteint son maximum sont appelées anti-noeuds ou ventres. On vérifiera facilement que la distance entre un noeud et un ventre est:

$$d_{noeud-ventre} = \frac{\pi}{2}\frac{v}{\omega} = \frac{\pi}{2k} \equiv \frac{\lambda}{4}$$

où $\lambda = 2\pi/k$ est la longueur d'onde. Dans une corde d'une longeur finie $L$, il faut que la réflexion à l'autre extrémité amène l'onde à se supersposer à l'onde initiale pour maintenir une onde stationnaire. Il y a différents cas particuliers. La Fig. 3 montre un de ces cas où une extrémité est fixée et l'autre est ouverte. C'est l'équivalent d'un tube ouvert d'une coté (clarinette) ou d'un cable coaxial alimenté à une extrémité et en court circuit à l'autre. La condition à remplir pour avoir une onde stationaire est:

$$ L = \frac{(2 n +1)\lambda}{4}$$

Modes de résonnance d'une onde stationnaire avec le mode noeuds-ventres. (Source: ©Cleaning Technologies Group)

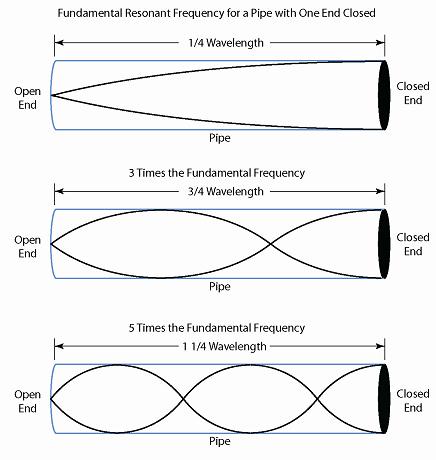
On peut avoir aussi le cas d'un tuyau ouvert aux deux bouts (flûte), comme un cable coaxial non terminé, ou encore une tige vibrante laissée libre à ses deux extrémités (voir Fig. 4). Dans ce cas ici, la condition à remplir est:

$$ L = \frac{(2n)\lambda}{4}$$

Modes de résonnance d'une onde avec le mode ventre-ventre. (Source © Cleaning Technologies Group)

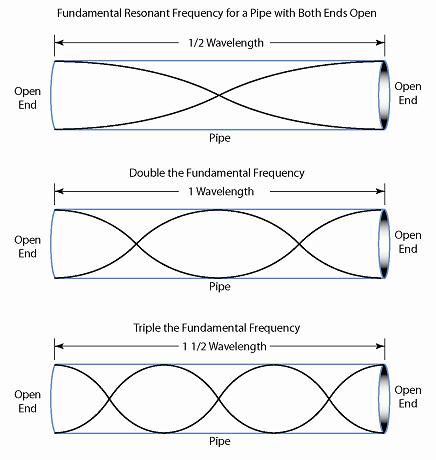
Question: Quelle-est la condition à remplir pour la longueur $L$ pour le cas correspondant à une tige fixée à ses deux extremités (noeud-noeud) ?

Le son comme une onde

Contrairement aux ondes bien connues sur une corde ou sur une vague, le son n'est pas transmis à travers une onde transverse, mais à travers une onde longitudinale de pression. En fait, il peut être décrit par une onde longitudinale de déplacement d'air ou une onde longitudinale de pression d'air.

Une onde sonore dans une colonne d'air. (Source: Hyperphysics).

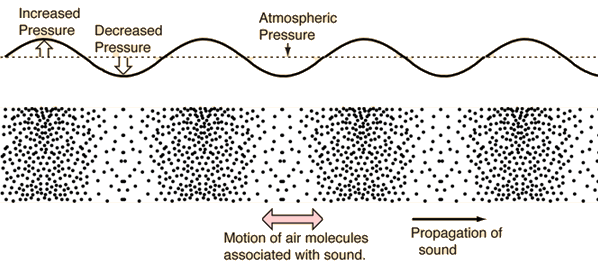
Le son passant à travers un fluide au repos entraîne des fluctuations de pression autour de la pression d'équilibre $p_0$, mais également des fluctuations corrélées de masse volumique autour de $\rho_0$ et de vitesse locale autour de $\vec{u}(\vec{r}) = \vec{0}$. Si on considère que le fluide au repos est faiblement perturbé par des ondes sonores usuelles (ce qui sera vérifié à posteriori), on peut trouver une équation générale reliant ces fluctuations sur base de l'hydrodynamique des fluides, traitant les fluctuations au premier ordre. L'équation de continuité

\begin{equation} \frac{\partial \rho}{\partial t} + \bar{\nabla}.\rho \bar{u}=0 \label{1} \tag{1} \end{equation}

devient au premier ordre

\begin{equation} \frac{\partial \rho}{\partial t} + \rho_0\bar{\nabla}. \bar{u}=0 \label{2} \tag{2} \end{equation}

L'équation d'Euler (équation du mouvement des fluides non visqueux)

\begin{equation} \rho [\frac{\partial \bar{u}}{\partial t} + (\bar{u}.\bar{\nabla}) \bar{u}]=-\bar{\nabla}p \label{3} \tag{3} \end{equation}

devient au premier ordre

\begin{equation} \rho_0 \frac{\partial \bar{u}}{\partial t} =-\bar{\nabla}p \label{4} \tag{4} \end{equation}

Dérivant l'éq. (\ref{2}) par rapport au temps et combinant avec l'éq. (\ref{4}), on trouve

\begin{equation} \frac{\partial^{2}\rho}{\partial t^2}=-\rho_0 \left(\frac{\partial }{\partial t}\right) \bar{\nabla}.\bar{u} \\ = - \bar{\nabla}.(\rho_0\frac{\partial \bar{u}}{\partial t})=\bar{\nabla}.\bar{\nabla} p=\nabla^2 p \label{5} \tag{5} \end{equation}

Enfin, on tire localement de l'équation d'état

\begin{equation} \rho -\rho_0=\left(\frac{\partial \rho}{\partial p}\right)_0 (p-p_0) \label{6} \tag{6} \end{equation}

où $\left(\frac{\partial \rho}{\partial p}\right)_0$ caractérise la compressibilité du fluide. Combinant les éqs (\ref{6}) et (\ref{5}), on obtient finalement

\begin{equation} \left(\frac{\partial \rho}{\partial p}\right)_0 \left(\partial^2 p/\partial t^2\right)= \nabla^2 p \label{7} \tag{7} \end{equation}

qui, mathématiquement, est bien une équation d'onde. Une solution de type onde plane de pression $p-p_0=A \sin{(\omega t-\bar{k}.\bar{r})}$ est solution de l'éq. d'onde si la vitesse de l'onde $c_s$

\begin{equation} c_s=\frac{\omega}{k}=\sqrt{\left(\frac{\partial p}{\partial \rho}\right)_0}=(\frac{1}{\rho_0 \chi})^{\frac{1}{2}} \label{8} \tag{8} \end{equation}

où $\chi$ est le coefficient de compressibilité du fluide. La théorie, dans la mesure où elle néglige totalement les effets visqueux, prédit que les ondes de pression se propagent dans un fluide sans amortissement et sans dispersion (les ondes de fréquences différentes ont toutes la même vitesse). Il convient de noter qu'en fait, toute fonction de type

\begin{equation} \delta p(x,t)=f(t \pm \frac{x}{c_s}) \label{9} \tag{9} \end{equation}

satisfait l'équation générale (\ref{7}), ce qui permet de mesurer la vitesse de propagation du son à partir de signaux plus diversifiés que des ondes sinusoïdales.

Montage experimental

La figure 5 montre le montage expérimental. Le mouvement mécanique vibratoire de la membrane d'un haut parleur communique à l'air une perturbation longitudinale dans un tuyau de longueur $L$ orienté perpendiculairement à la membrane.

Montage général.

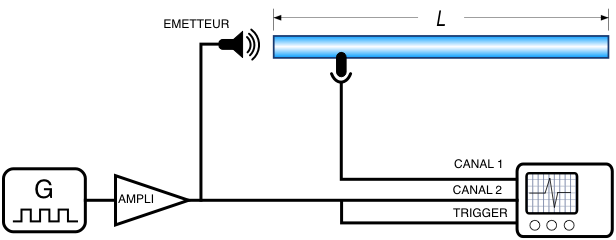
Un micro est placé à une distance $h \ll L$ de l'émetteur. Si l'axe du tuyau est pris pour axe $x$, la perturbation de pression émanant de l'émetteur sera du type $p(x,t)=f(t-\frac{x}{c_s})\equiv f(z)$. Pour faire le lien entre perturbations de pression et de densité avec leur origine (déplacement de l'air en contact avec la membrane émettrice) et leur détection par un micro (mise en mouvement mécanique de la membrane suite à une perturbation longitudinale de l'air avoisinant), il convient d'intégrer dans notre description le (faible) déplacement longitudinal $s(x,t)$ de l'air par rapport à l'air au repos, pour une tranche d'air située en x dans l'état de référence. Comme $u_x=\frac{\partial s}{\partial t}$, on a, en vertu de l'éq. (\ref{2})

\begin{equation*} \frac{\partial u_x}{\partial t}= \frac{\partial^2 s}{\partial t^2}=- \rho_0^{-1}\frac{\partial p}{\partial x} \label{eq:trois} \end{equation*}

Ceci implique que les fonctions $s(x,t)$ et $u_x(x,t)$ doivent être, tout comme les fluctuations de pression et de densité des fonctions de l'argument $z=t-\frac{x}{c_s}$. Ainsi, si la membrane exécute un mouvement longitudinal de type $g(t)$ identifié à un mouvement de l'air à l'origine $s(0,t)$, on aura selon l'éq precedent, les relations

\begin{eqnarray*} s(x,t)&=&g(t-\frac{x}{c_s})\\ u_x(x,t)&=&g'(t-\frac{x}{c_s})\\ p(x,t)-p_0&=&c_s \rho_0 g'(t-\frac{x}{c_s})=(\frac{\rho_0}{\chi})^{\frac{1}{2}}g'(t-\frac{x}{c_s})\\ \rho(x,t)-\rho_0&=& c_s \rho_0 \left(\frac{\partial \rho}{\partial p}\right)_0 g'(t-\frac{x}{c_s})= \chi^{1/2} \rho_0^{3/2} g'(t-\frac{x}{c_s}) \end{eqnarray*}

Le lien entre la fonction $f(z)$ qui caractérise la pression et $g(z)$ qui caractérise le déplacement de l'air est donc donné par

\begin{equation*} f(t \mp \frac{x}{c_s})= \pm \rho_0 c_s g'(t \mp \frac{x}{c_s}) \label{eq:cinq} \end{equation*}

Cas particuliers et effets de bout

Prenons le cas le plus simple d'un signal carré de fréquence suffisamment basse (en pratique $\nu<<60Hz$) pour que la durée de l'aller-retour du signal soit inférieure à sa demi-période (durée d'un créneau du signal carré). Prenant pour origine du temps le moment où le signal fait sa marche de $0$ à $A$, la fonction traduisant le déplacement de la membrane s'écrit $g(t)=A \theta(t)$ où $A$ est une amplitude et la fonction de Heaviside $\theta(t)=0$ si $t<0$ et $\theta(t)=1$ si $t>0$.

\begin{eqnarray*} s(x,t) &=& A \theta(t-\frac{x}{c_s}) \\ \delta p(x,t) &=& A (\frac{\rho_0}{\chi})^{1/2} \delta(t-\frac{x}{c_s}) \label{eq:six} \end{eqnarray*}

Signal aller.

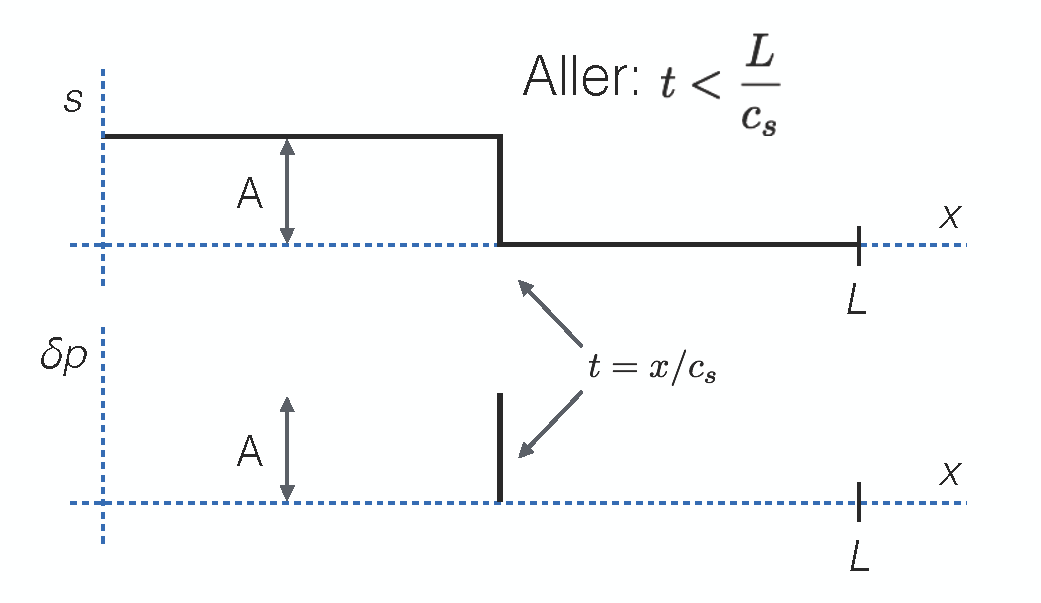
La Fig. 7 montre $s(x,t)$ et $\delta p(x,t)$ pour un temps inférieur à $L/c_s$.

Tuyau bouché à son extrémité

Dans ce cas, la perturbation qui arrive au bout du tuyau doit rebondir sur la paroi. Ceci peut être exprimé avec une condition aux bords de type $s(L,t)=0$ pour $t$ arbitraire. On voit que la solution de l'éq. anterieur n'est pas compatible avec la condition aux bords. La solution doit en fait comporter une perturbation se déplaçant dans le sens inverse, correspondant à la réflexion du signal au bout du tuyau. La solution satisfaisant les conditions aux bords, est ainsi

\begin{eqnarray*} s(x,t)&=& A \left[\theta(t-\frac{x}{c_s})-\theta(t-\frac{2L-x}{c_s})\right] \\ \delta p(x,t)&=& A \left(\frac{\rho_0}{\chi}\right)^{1/2} \left[\delta(t-\frac{x}{c_s})+\delta(t-\frac{2L-x}{c_s})\right] \label{eq:sept} \end{eqnarray*}

Signal retour: bout fermé.

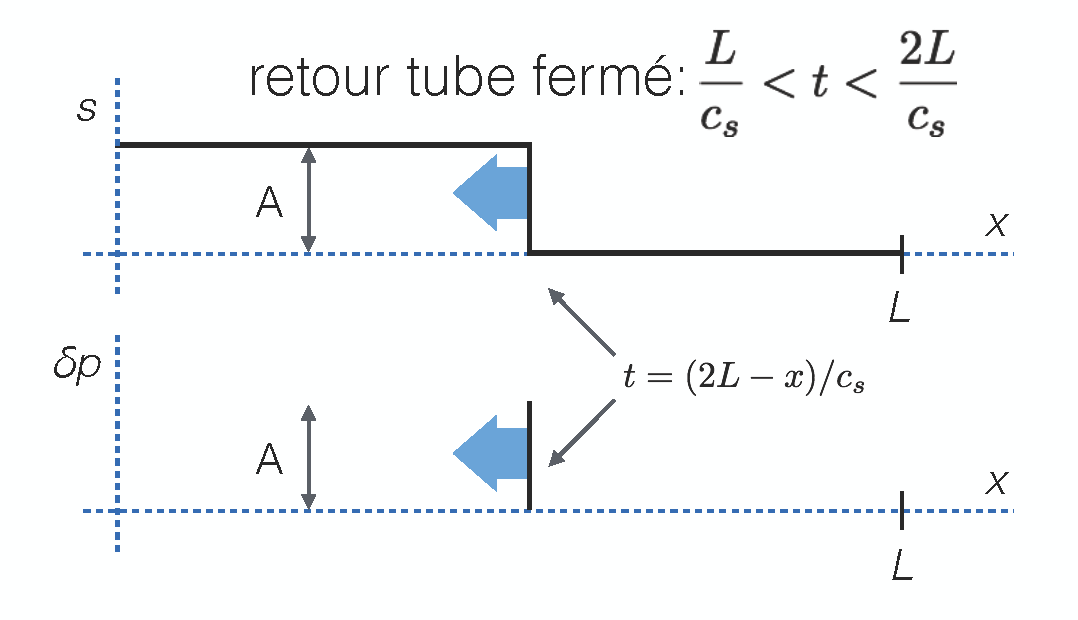
Le figure ci-dessus montre le signal, après réflexion de la perturbation sur le bout fermé du tube.

Tuyau ouvert à son extrémité

Dans ce cas, la perturbation qui arrive au bout du tuyau débouche sur un milieu continu à 3D où règne la pression $p_0$. Ceci peut être exprimé avec une condition aux bords de type $\delta p(L,t)=0$ pour $t$ arbitraire. La solution doit en fait à nouveau comporter une perturbation se déplaçant dans le sens inverse, correspondant à la création d'une perturbation compensant le signal original arrivant au bout du tuyau. La solution satisfaisant les conditions aux bords, est ainsi

\begin{eqnarray*} s(x,t)&=& A \left[\theta(t-\frac{x}{c_s})+\theta(t-\frac{2L-x}{c_s})\right] \\ \delta p(x,t)&=& A (\frac{\rho_0}{\chi})^{1/2} \left[\delta(t-\frac{x}{c_s})-\delta(t-\frac{2L-x}{c_s})\right] \label{eq:huit} \end{eqnarray*}

Signal retour: bout ouvert.

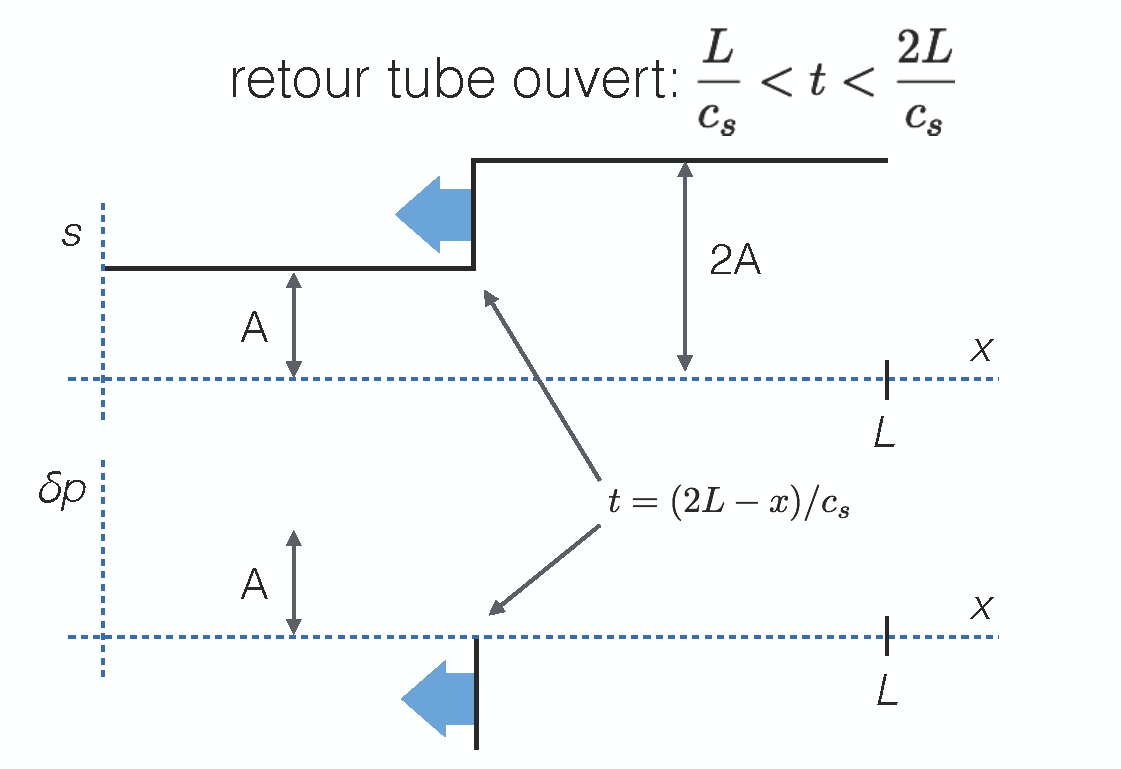
Nature du coefficient de compressibilité

En thermodynamique, le coefficient de compressibilité $\chi$ traduit la variation de densité avec la pression, autour du point de référence, selon un processus réversible. Théoriquement, un processus réversible est en fait un processus modèle, à savoir un processus infiniment lent reliant une suite d'états d'équilibre. Ceci est une approximation dans le cas présent, mais cohérent avec notre hypothèse de négliger l'effet des forces visqueuses qui donnent lieu généralement à un comportement irréversible. Or un état d'équilibre est caractérisé par deux variables thermodynamiques indépendantes, ce qui implique que la relation dont nous avons besoin ici est $\rho=f(p,T)$. Il y a donc une infinité de façons différentes de modifier la pression, dont les deux cas les plus courants étant les processus isotherme ($T = cte.$) et adiabatique (sans échange de chaleur, soit à entropie $S = cte.$). Pour ces deux processus, on obtient dans l'approximation des gaz parfaits, les expressions suivantes (voir cours):

\begin{eqnarray*} \chi_T&=& - \frac{1}{V}\left(\frac{\partial V}{\partial p}\right)_T=\frac{M_m}{\rho RT} \\ \chi_S&=& - \frac{1}{V}\left(\frac{\partial V}{\partial p}\right)_S=\frac{M_m}{\rho RT}\frac{C_v}{C_p} \label{eq:neuf} \end{eqnarray*}

où $M_m$ est la masse molaire du gaz, $R = 8.31$ J/K est la constante des gaz parfaits, le rapport des chaleurs spécifiques à pression et volume fixés étant $C_p/C_v $ = 5/3 pour les molécules sphériques ou $C_p/C_v$ = 7/5 pour les molécules linéaires (voir cours).

Travail à effectuer

Analyse préliminaire: émetteur et micro

Connectez l'émetteur à un générateur et choisissez un signal carré de fréquence suffisamment basse, à observer sur l'oscillo. Après avoir connecté le micro à l'oscillo, visualisez le signal perçu. Discutez du lien entre signal émis et signal perçu par le micro: ce dernier mesure-t-il $s$ ou $\delta p$? Placez ensuite le micro le long du tuyau dans la niche prévue et disposez le tuyau contre l'émetteur, l'axe du tuyau étant placé perpendiculairement à la membrane émettrice. Discutez la forme générale du signal. Y a-t-il un ou deux passages du signal au niveau du micro, ou peut-être encore plus? Comment interprétez vous la séquence de signaux observés?

Analyse de la propagation du son dans le tuyau fermé à son extrémité

Le bout du tuyau étant fermé par un bouchon, les signaux aller-retour sont ils du même type au niveau de leur observation par le micro? Y a t il accord avec les prédictions théoriques?

Analyse de la propagation du son dans le tuyau ouvert à son extrémité

Le bout du tuyau étant ouvert, les signaux aller-retour sont-ils du même type au niveau de leur observation par le micro? Y a t il accord avec les prédictions théoriques?

Mesure de $c_s$, la vitesse du son dans l'air

Pour mesurer la vitesse du son, on mesure le temps mis par le signal pour faire une distance connue, en l'occurence un aller-retour au départ du micro, soit sur une distance $d=2(L-h)$. Mesurez la distance $L-h$ avec précision et ensuite le temps entre les passages successifs de la perturbation au micro, à l'aide de l'oscilloscope en mode balayage. Que trouvez vous pour la vitesse du son dans l'air? Quelle est l'erreur expérimentale associée? Cette vitesse du son mesurée est-elle compatible avec les prédictions théoriques (n'oubliez pas que la vitesse du son dépend de la température du milieu) ? Pouvez-vous en particulier apprécier, sur la base d'une comparaison quantitative de la valeur expérimentale de $c_s$ avec les prédictions théoriques, si les compressions ou expansions de l'air sont plutôt isothermes ou adiabatiques?

Mesure de la vitesse du son dans l'hélium (He)

De l'helium peut être introduit dans le tuyau à partir d'une bonbonne d'helium comprimé. Faites la même mesure de temps entre les signaux successifs aller et retour au fur et à mesure que l'He chasse l'air pour y prendre sa place. Mesurez le temps limite (quand l'air au sein du tuyau est de l'helium pur). La valeur de $c_s$ correspondante est-elle compatible avec la prédiction théorique? Prenez toujours garde à avoir une prédiction théorique dépendant de la température.

Ondes sonores dans l'air

Les ondes sonores audibles par l'oreille humaine vont de 20 Hz à 20 kHz. Etant donné la vitesse du son, évaluez les longueurs d'ondes correspondantes. La longueur d'onde donne la taille des éléments de fluide qui se contractent ou se dilatent lors du passage de l'onde.

• Comparez la taille d'un élément de fluide qui se contracte ou dilate au libre parcours moyen des molécules dans l'air.
• Le processus de contraction ou dilatation est-il isotherme ou adiabatique pour les ondes sonores? Comparez le temps mis par la chaleur pour diffuser sur une distance de l'ordre de la taille d'un élément qui se contracte à la durée d'un cycle de contraction/dilatation. Qu'en concluez-vous? Quid dans le cas de la perturbation de type $\theta(t)$ étudiée pour mesurer $c_s$ expérimentalement?
• Y a-t-il finalement un refroidissement et un échauffement des zones dilatées ou contractées, respectivement? Si oui, quelle variation de température cela donnerait si les fluctuations de pression sont de l'ordre du $0,02$ millibar. La réponse à ces questions demande d'exploiter des concepts théoriques vus au cours.

Détection du signal de retour en utilisant la membrane de l'émetteur comme membrane de micro

En choisissant un signal impulsionnel (au lieu d'un signal carré) et en utilisant les possibilités de moyennage de signaux de l'oscillo, on peut observer le signal de retour, après un voyage aller retour de durée $2L/c_s$.

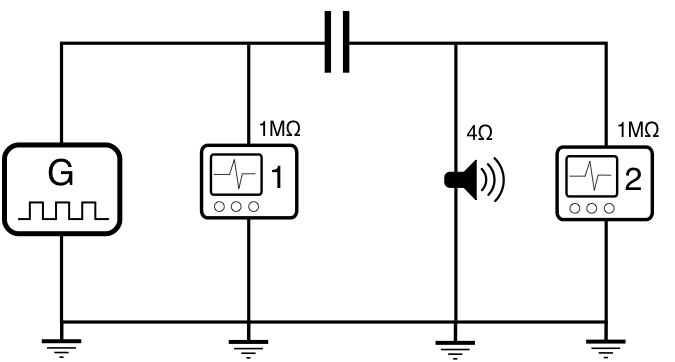
Une configuration commode pour réaliser cette mesure consiste à interposer un condensateur en série entre la sortie de l'ampli et le haut parleur . Il suffit alors d'observer le signal sur la membrane du haut parleur (un seul canal de l'oscillo). Le signal observé "au départ" comprend l'impulsion initiale, suivie de quelques oscillations vite amorties du HP (correspondant à sa fréquence propre de résonnance). A première vue, le signal en retour n'apparaît pas: c'est normal, il est beaucoup plus faible (rendement accoustique du HP). Pour le voir, il faut amplifier beaucoup plus fort; le signal initial dépasse alors (mais c'est sans conséquence) l'affichage, mais le signal en retour reste largement perdu dans le bruit. Les oscillos digitaux offrent une solution élégante (et fréquemment utilisée en traitement du signal): en appuyant sur le bouton acquisition, on peut choisir de prendre la moyenne d'un nombre de répétitions (4,16,64,128). On voit alors que le bruit aléatoire s'estompe dans la moyenne, tandis que le signal se révèle clairement. Réaliser cette mesure en complément (et pour comparaison avec la manip similaire portant sur la propagation d'un signal électrique dans un coax).

Montage général.

---

Revision J.A. Aguilar 2016

J.P Ryck 2007