Laboratoire d'optique

ATENTION:

Ne JAMAIS regarder directement le faisceau laser. Ca peut endommager vos yeux !

Partie 1: L'optique géométrique

But de la manipulation:

Introduction à l'optique géométrique et à la polarisation.

Préparation

Avant de commencer cette expérience, il vaut mieux être familier avec les différentes notions telles que les lentilles divergentes et convergentes, les images réelles et virtuelles, etc. Pour cela, l'étudiant est invité à consulter la bibliographie.

Détermination de la distance focale d'une lentille convergente

Pour les manipulations suivantes utilisez toujours la même lentille afin de verifier le different moyens de détermination de la distance focale.

Par une relation géométrique

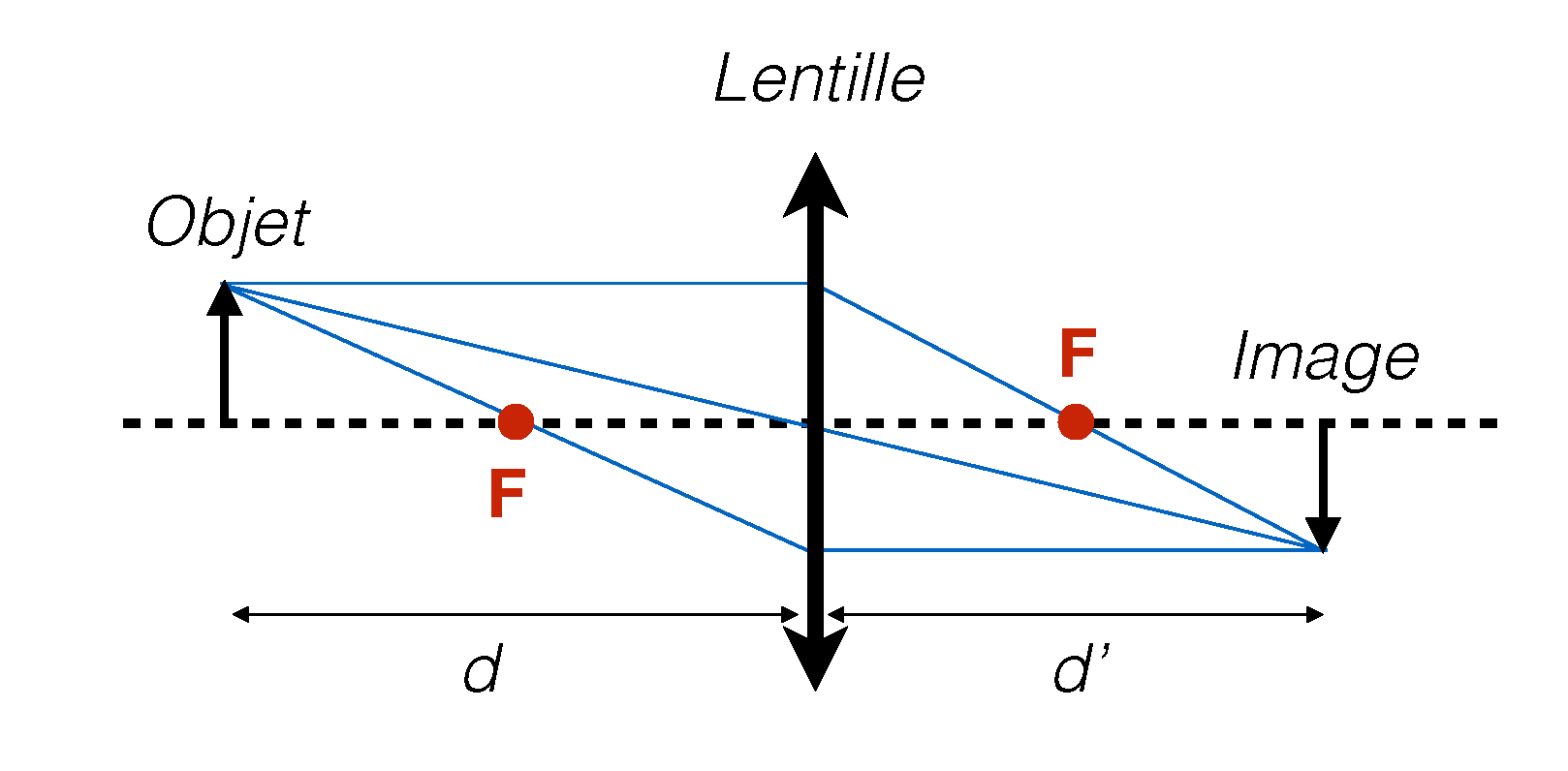
La relation géométrique $\frac{1}{\mathcal{f}} = \frac{1}{d} + \frac{1}{d^\prime}$ relie la distance focale d'une lentille $\mathcal{f}$ avec les distances, $d, d^\prime$ de l'objet et de l'image à la lentille. Aussi longtemps que $d, d^\prime$ sont positifs, l'image est une image réelle comme montré sur la figure 1. Par contre, si $d < \mathcal{f}$ alors $d^\prime$ est negatif ce qui correspond à une image virtuelle.

Procedure: Mesurer les distances $d$ et $d^\prime$ quand l'image sur un tableau est nette et définie. En déduire $\mathcal{f}$ avec les incertitudes. Répeter la mesure plusieurs fois avec différentes valeurs de $d$. Calculer la valeur moyenne de la distance focale $\mathcal{f}$ et son erreur statistique.

Question: Observer ce qui se passe quand $d=\mathcal{f}$?

Dispositif expérimental.

Par la méthode du miroir

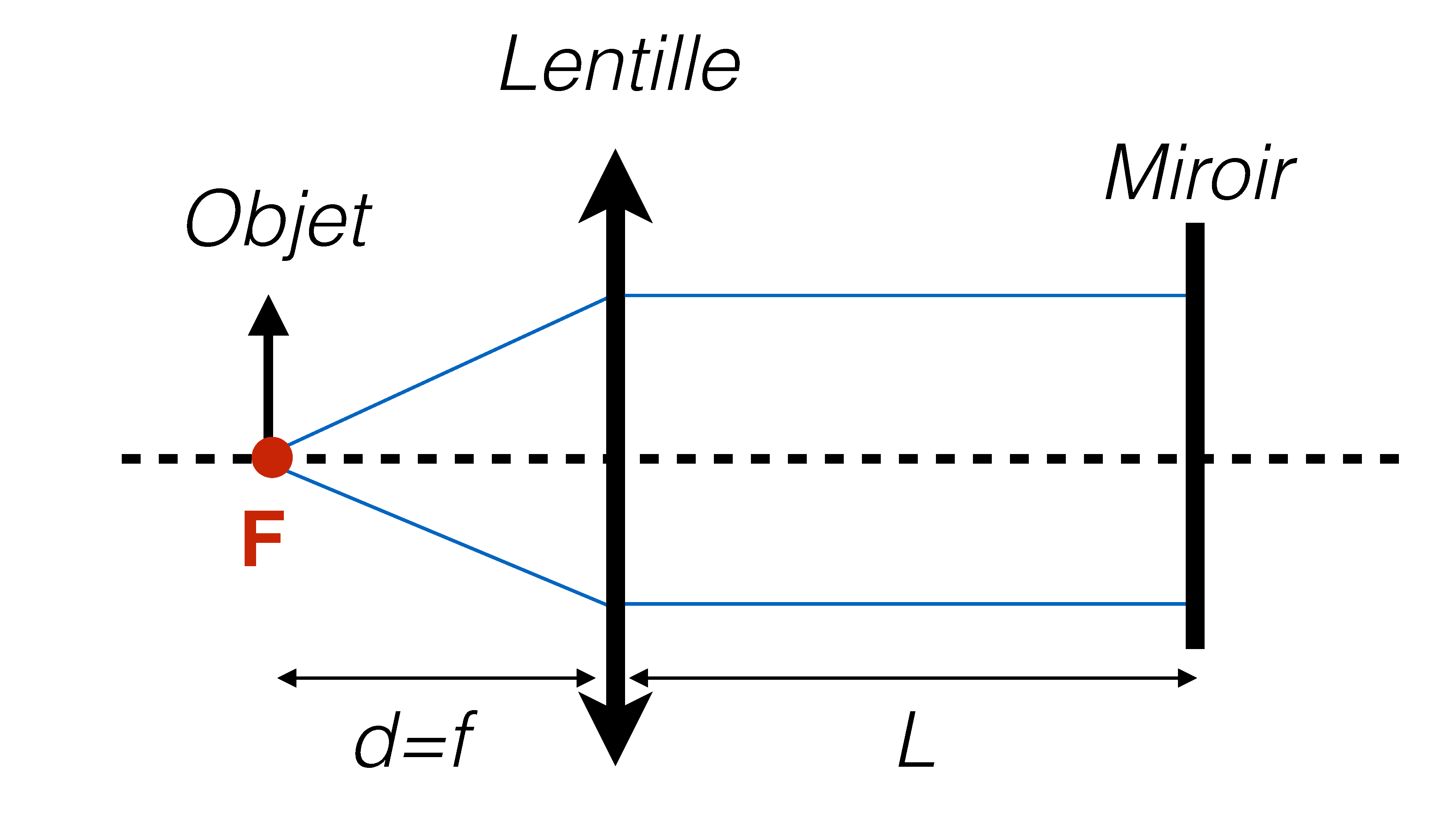
Lorsque $d =\mathcal{f}$, l'image est à l'infini. Si un miroir est placé comme montré sur la figure 2, l'image est redirigée sur le plan de l'objet. Pour que nous puissions voir l'image et l'objet au même endroit, nous allons utiliser comme objet une diapositive semi transparente avec la moitié couverte par un papier blanc. Pour faciliter la visualisation de l'image, nous pouvons incliner un peu le miroir pour envoyer l'image sur le papier

Procédure: Déterminer $\mathcal{f}$ et son erreur. Faire au mois 3 mesures.

Question: Pourquoi l'image sur le papier est elle inversée par rapport à l'objet? Pourquoi l'image devient elle plus petit lorsque'on éloigne le miroir?

Dispositif expérimental avec miroir.

Avec les rayons parallèles

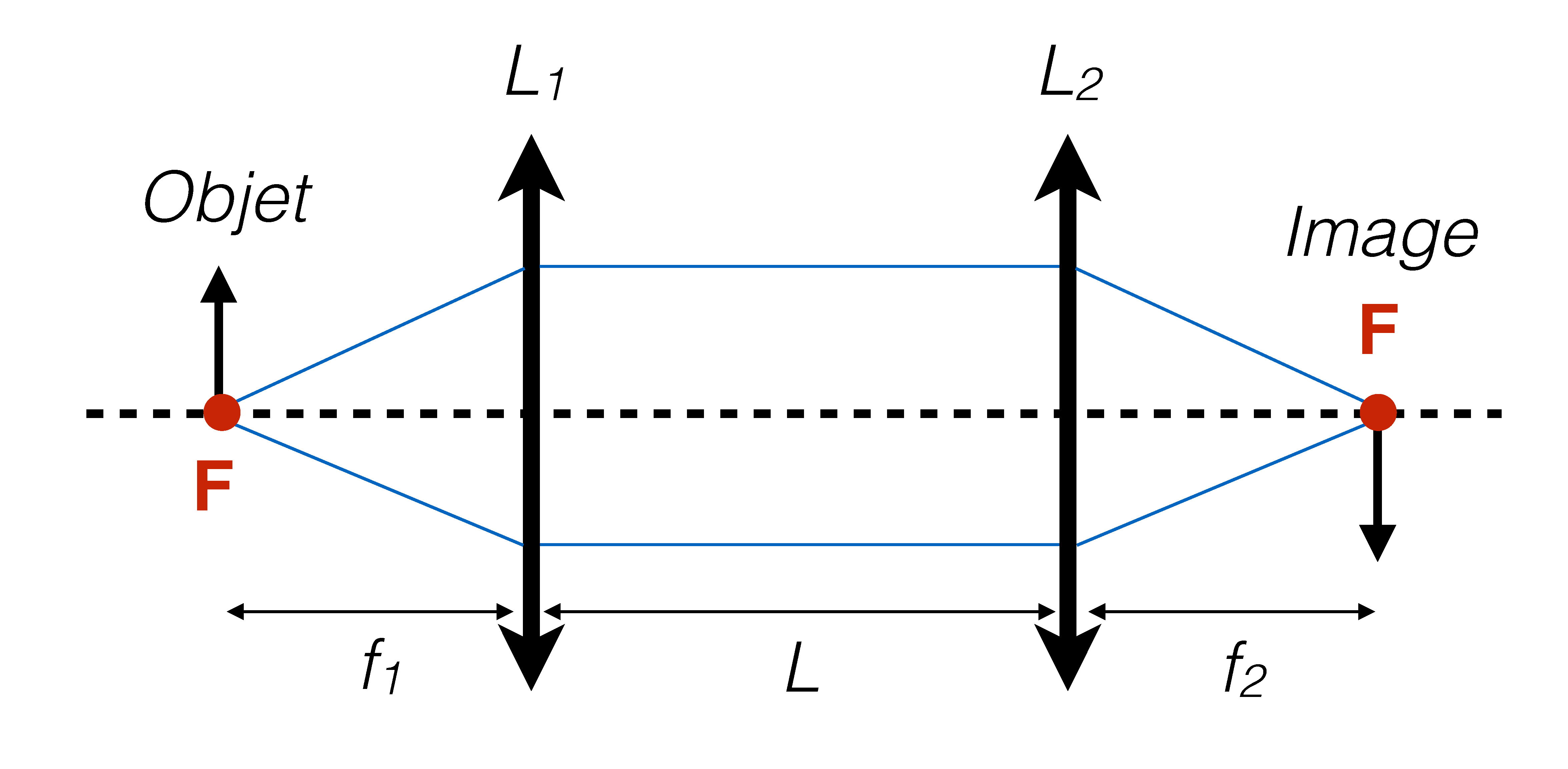
Comme vu dans la section précédente, en placant un objet à la distance focale $\mathcal{f}_1$ d'une lentille $L_1$, nous obtenons des rayons parallèles de lumière. Si on place une seconde lentille $L_2$ après, l'image sera formée à la distance $d = \mathcal{f}_2$. En mesurant $d$ nous pouvons obtenir $\mathcal{f}_2$. Dans cette expérience, la taille de l'objet et celle de l'image sont reliés par l'équation :

$$G =\frac{l_{obj}}{l_{image}} = \frac{\mathcal{f}_1}{\mathcal{f}_2}$$

Où $G$ s'appelle le grossissement de système optique.

Procédure: Pour obtenir des rayons parallèles du lumière de bonne qualité, nous utiliserons un objectif photographique au place de la lentille $L_1$. Un objectif photographique n'est pas une simple lentille, mais se compose de différentes lentilles qui corrigent les abérations présentent avec une lentille simple. Mesurez $d$ et en déduire $\mathcal{f}_2$ et son insertitude. Comparez les méthodes précédents pour obtenir $\mathcal{f}_2$. Vérifier aussi la relation entre la taille de l'objet et de l'image, $G$

Dispositif expérimental avec des rayons parallèles.

Détermination de la distance focale d'une lentille divergente et instruments optiques simples

Détermination de la distance focale d'une lentille divergente en utilisant une image virtuelle.

Suivant la relation entre la distance focale et la distance de l'objet et de l'image montrée précédemment :

$$\frac{1}{\mathcal{f}} = \frac{1}{d} + \frac{1}{d^\prime}$$

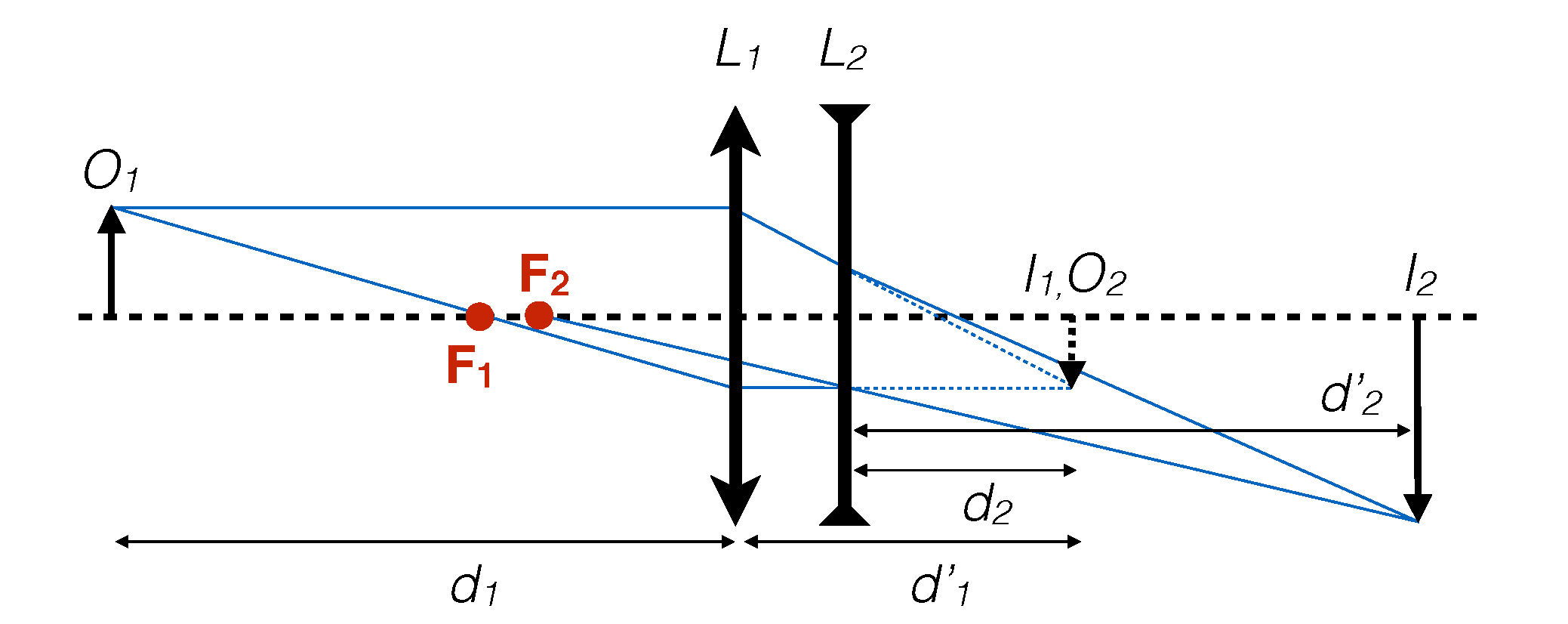
Dans notre convention, nous savons que quand $\mathcal{f} < 0$, la lentille est divergente et l'image créée n'est pas une image réelle d'un objet réel. Pour mesurer la distance focale d'une lentille divergente $L_2$ nous allons utiliser une lentille convergente, $L_1$ qui va créer une image réelle $I_1$ d'un objet $O = O_1$. Nous plaçons la lentille divergente pour que l'image $I_1$ créée par $L_1$ soit l'objet virtuel $O_2$ de la lentille divergente. Dans cette configuration l'image $I_2$ créée par la lentille divergente sera une image réelle (voir figure 4).

Procédure: Réalisez le dispositif indiqué sur la figure 4 et déterminer la distance focale de la lentille divergente.

Dispositif expérimental avec une lentille divergente.

Création d'un zoom

Nous utilisons le dispositif de la section Avec les rayons parallèles. Nous allons remplacer la seconde lentille $L_2$ par une combinaison de deux lentilles, une convergente $L_2$, et une divergente $L_3$ à une distance $D$. En variant cette distance $D$ (avec $L_2$ fixée), la combinaison des lentilles $L_2$ et $L_3$ va nous donner une lentille avec une distance focale variable.

Dispositif expérimental d'un zoom.

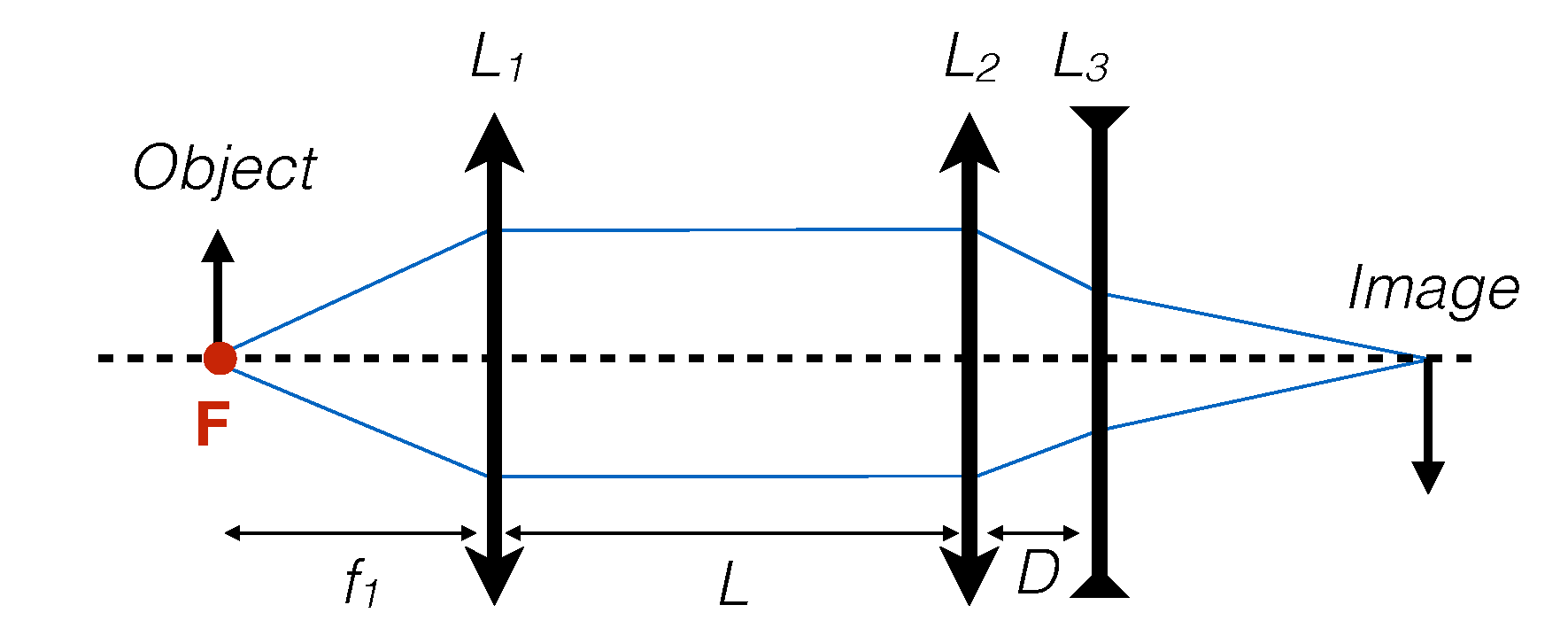
En effet, pour $D\rightarrow 0$, les puissances $P=1/\mathcal{f}$ s'ajoutent algébriquement:

$$\frac{1}{\mathcal{f}_{equiv}} = \frac{1}{\mathcal{f}_2} + \frac{1}{\mathcal{f}_3}$$

où $\mathcal{f}_{equiv}$ est la focale de la lentille équivalente $L_2$ + $L_3$.

Procédure: Déterminer expérimentalement la relation entre D et la focale équivalent de la paire $L_2$, $L_3$. Mesurez le grossissement $G$ pour différent valeurs de $D$, ainsi que les incertitudes.

Question: Tracez la courbe expérimentale du grossissement $G$ en fonction de $D$, le comportement est-il linéaire? Que passe il lorsque $D = \mathcal{f}_2$

Création d'autres instruments d'optique

Selon le temps disponible, vous êtes invités à realizer des modèles d'intruments d'optiques simples. Ne pas hésiter à chercher sur Internet des possibles modèles: lunette astronomoque, microscope, etc. Décrivez le fonctionnement dans votre rapport.

Partie 2: Polarisation, milieux anisotropes

Polarisation

Préparation:

Pour une information complète sur ce sujet, l'étudiant est invité à lire le chapitre 10 du cours de Mr Haelterman PHYS-H-302. Les autres sources sont :

• Physics classroom. Un site web avec différentes informations en physique à un niveau de vulgarisation.

• Wikipedia on polarization. Wikipedia peut parfois être très utile pour une première approche d'un sujet.

• Polarizer Page wikipedia en anglais au sujet des polariseurs.

La loi de Malus

Lorsqu'une lumière non polarisée voyage à travers deux polariseurs linéaires, la lumière résultante est fort atténuée. Généralement, nous appelons le deuxième polariseur orienté d'un angle $\theta$ par rapport au premier polariseur l'analyseur. La loi de Malus nous dit que l'intensité lumineuse après l'analyseur est donnée par :

$$I(\theta) = I_0\cos^2\theta$$

où $I_0$ est la l'intensité maximum transmise.

Procédure: Utilisez le dispositif dans la figure 6 pour étudier la loi de Malus. Faites un graphique de l'intensité lumineuse en fonction de $\cos^2\theta$ où $\theta$ est l'angle entre le polariseur et l'analyseur.

Question: Dans le graphique, passe la ligne par 0? Pourquoi pas?

La qualité du polariseur peut être mesurée comme une fonction du rapport d'extinction $\frac{I_{max}}{I_{min}}$. Les meilleurs polariseurs ont un rapport d'extinction de $10^{-6}$. Déterminez le rapport d'extinction de l'ensemble polariseur-analyseur.

Dispositif expérimental pour l'étude de la loi de Malus.

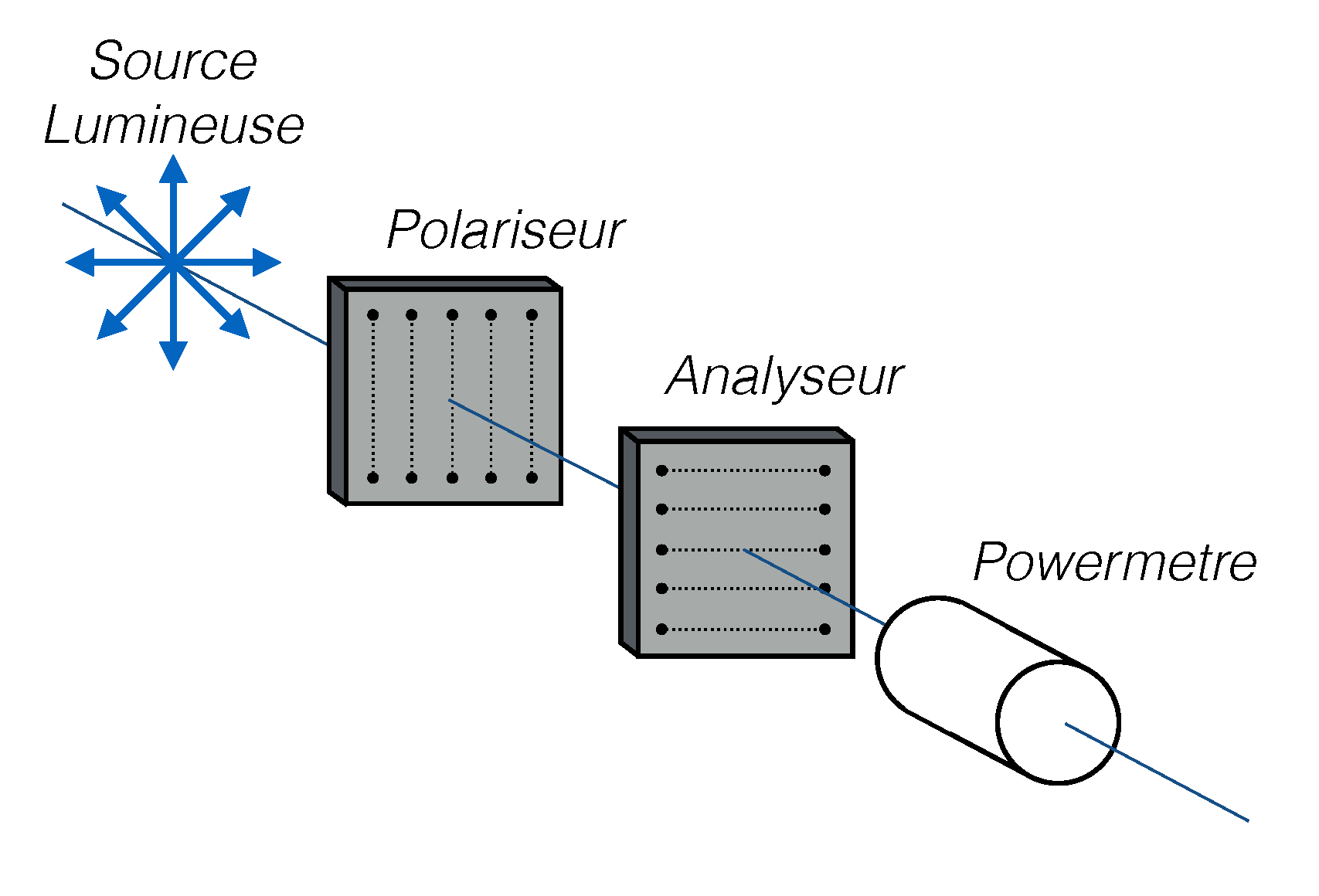
Remarque: Soyez sur que la lumière qui arrive sur le powermetre vient de la source et n'est pas de la lumière ambiante.

Angle de Brewster

La lumière réfléchie sur un diélectrique est partiellement polarisée. A l'angle d'incidence appelé angle de Brewster, la lumière réfléchie est complètement polarisée. Ceci intervient par exemple lors de réflections sur les fenêtres, surfaces d'eau, etc. Et c'est la raison pour laquelle les polariseurs sont souvent utilisés en photographie pour éliminer la lumière venant des réflections. Un exemple est montré sur la Fig. 7.

Deux photographies, l'une prise avec un polariseur, l'autre sans. (Source: via Wikimedia Commons.)

L'angle de Brewster est donnée par l'expression:

$$\theta_B = \arctan \frac{n_2}{n_1}$$

où $\theta_B$ est l'angle de Brewster défini comme l'angle incident par rapport à la normale, et $n_1$ et $n_2$ sont les indices de réfraction des milieux incidents et diélectriques (voir figure 8).

Lumière réfléchie à l'angle de Brewster sur un milieu diélectrique. (Source: By Pajs via Wikimedia Commons)

Procédure: Mesurez l'angle de Brewster pour une vitre noire. Placez une polarizator entre la source et le vitre. Tournez le vitre jusqu'à ce que la lumière réfléchie est minime. Répétez la mesure 3 fois avec les incertitudes. Comparez l'angle mesuré avec la prédiction théorique de la formule ci dessus (cherchez l'indice de réfraction de le vitre noire dans Internet).

Modèle de mécanique quantique

Imaginez que nous installions le polariseur et l'analyseur dans une configuration telle que l'intensité de la lumière est minimale. Si nous insérons un 3e polariseur entre les deux, comment l'intensité lumineuse dépendra t elle de l'orientation du 3e polariseur ? C'est en fait un modèle utilisé en mécanique quantique qui explique les mesures consécutives.

Question: Avec une série de $N$ polariseurs décalés (chacun l'un par rapport à l'autre) d'un angle $\theta/N$, quelle est l'intensité quand $N\rightarrow \infty$?

Milieux anisotropes, lames demi ondes, lames quart d'ondes

Introduction

Certains matériaux ont une structure interne qui modifie l'état de polarisation de la lumière qui les traverse. Le quartz cristalin est un exemple de ces matériaux ou milieux anisotropiques.

Cela peut se produire quand l'indice de réfraction du matériau diffère selon la direction. Par exemple, pour la lumière voyageant selon l'axe z, les ondes polarisées selon l'axe x verront un indice du milieu $n_x$, tandis que la lumière polarisée delon l'axe y ferront l'expérience d'un indice de réfraction $n_y$. Ceci est appelé lame à retard. En choisissant l'épaisseur de la lame, on peut faire en sorte que la lumière polarisée dans une direction soit retardée de $\lambda/2$, ceci est appelée une lame demi onde. De la même façon, si le retard est de $\lambda/4$, la lame est appelée une lame quart d'onde.

Une lame demi onde. La lumière polarisée linéairement entrant en onde plane peut être décomposée en deux ondes, parallèle (en vert) et perpendiculaire (bleu) à l'axe optique de la lame à retard. Dans la lame, les ondes parallèles vont se propager plus lentement que celles perpendiculaires. A la sortie de la lame, l'onde parallèle est exactement décalée de la moitié d'une longueur d'onde par rapport à l'onde perpendiculaire, et l'onde résultante (en rouge) est polarisée orthogonalement par rapport à l'onde entrante.

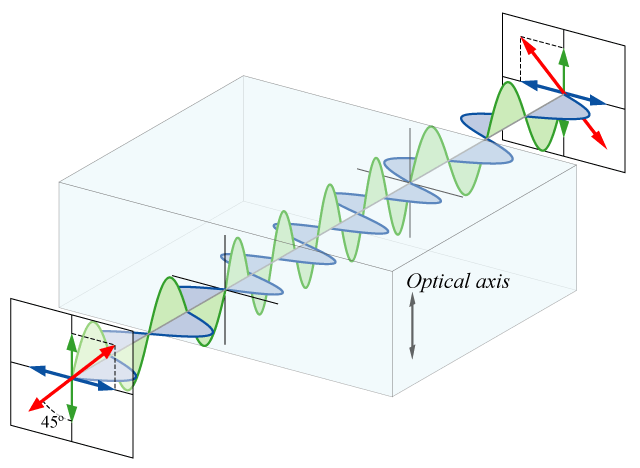
Préparation

Nous allons définir nos axes de telle manière que si une onde traverse l'axe z, elle possède un champ électrique ${\vec{E}}$ et un champ magnétique ${\vec{B}}$ comme montré sur la figure où $\vec{E}\perp\vec{B}$.

Onde électromagnétique se propageant le long de l'axe z. (Source: By P.wormer via Wikimedia Commons

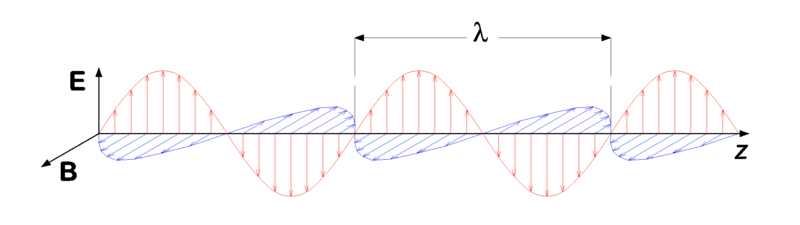
Le champ $\vec{E}$ peut s'exprimer comme :

$$\vec{E}(t, z) = \vec{E_0}\sin(\omega t-kz +\phi)$$

où $\phi$ est simplement une constante de phase. Ici pour une polarisation linéaire $\vec{E_0}$ est constant :

$$\vec{E_0} = E_{0x}\vec{1_x} + E_{0y}\vec{1_y}$$

où $\vec{1_x}$ et $\vec{1_y}$ sont les vecteurs unitaires directeurs des axes x et y. La vitesse de propagation est obtenue par les valeurs de $z$, $t$ et $\phi$ pour lesquelles le champ eléctrique est constant :

$$\begin{align*} \omega t - kz + \phi &= \rm{constant} \\ z &= \omega/k \cdot t \equiv vt \\ \omega &= 2\pi \nu \\ k &= 2\pi/\lambda \\ \omega/k &= \lambda \nu = v \end{align*}$$

Dans le vide, nous avons $v =c$ et dans un milieu homogène $ v = c_{mileu} < c$. Dans un milieu anisotrope, la vitesse dépend de l'orientation (polarisation) de $\vec{E}$ par rapport au cristal.

Milieu anisotrope, lame mince

Considérions une fine lame avec des faces parallèles d'une épaisseur $d$. Cette lame a deux directions principales et nous allons vérifier que la lumière polarisée dans chacune de ces deux directions reste polarisée mais que la vitesse de propagation est différente. Pour rendre les choses simples, nous allons assumer que ces deux directions coincident avec les axes x et y. Le champ électrique avant d'entrer dans la lame peut s'exprimer comme :

$$ \vec{E}(t,z) = (E_{0x}\vec{1_x} + E_{0y}\vec{1_y})\cdot \sin(\omega t-kz +\phi)$$

A l'intérieur de la lame, cependant, les deux composants voyagent à différentes vitesses ($k_x = \omega /c_x, k_y = \omega /c_y$):

$$ \vec{E}(t,z) = E_{0x}\vec{1_x} \sin(\omega t-\frac{\omega}{c_x}z +\phi) + E_{0y}\vec{1_y} \sin(\omega t-\frac{\omega}{c_y}z +\phi)$$

A la sortie de la lame, $z = d$, nous avons:

$$ \vec{E}(t,z=d) = E_{0x}\vec{1_x} \sin(\omega t-\frac{\omega}{c_x}d +\phi) + E_{0y}\vec{1_y} \sin(\omega t -\frac{\omega}{c_y}d +\phi)$$

Après ça, les deux composantes continuent à se propager librement. La différence de phase entre les deux composantes :

$$\alpha = \omega \left(\frac{d}{c_x} - \frac{d}{c_y}\right)$$

Si nous choisisons arbitrairement une constante de phase initiale de $\phi = \omega d/c_x$, nous pouvons réécrire l'équation à $z = d$ comme :

$$ \vec{E}(t,z=d) = E_{0x}\vec{1_x} \sin(\omega t) + E_{0y}\vec{1_y} \sin(\omega t+\alpha)$$

Notez que $\alpha$ ne dépend pas seulement de l'épaisseur $d$, mais aussi de la fréquence $\omega$. C'est pourquoi nous utiliserons comme source de lumière une lampe à sodium qui est presque monochromatique

Lame demi onde

On appelle un retardeur lame demi onde quand $\alpha = \pi$. Dans ce cas, l'équation ci dessus peut être réécrite comme :

$$ \vec{E}(t,z=d) = E_{0x}\vec{1_x} \sin(\omega t) - E_{0y}\vec{1_y} \sin(\omega t)$$

Les deux composants ont changé de signe.

Lame quart d'onde

Quand $\alpha = \pi/2$ nous avons une lame quart d'onde. Dans ce cas nous avons :

$$ \vec{E}(t,z=d) = E_{0x}\vec{1_x} \sin(\omega t) + E_{0y}\vec{1_y} \cos(\omega t)$$

Sous la condition que $E_{0x} = E_{0y}$ et en assumant que la polarisation initiale était de 45$^{\circ}$ par rapport aux deux directions principales, l'équation ci dessus est l'équation d'un cercle décrit par le champ électrique. Nous disons dans ce cas que l'onde électromagnétique a une polarisation circulaire (dans ce cas main-gauche)

Procédure : lames demi ondes et quart d'onde

• Placez la lame entre deux polarisateur croisés et identifiez les directions primaires de la lame. Utilisez le fait que si $\vec{E}(t, z = 0)$ est aligné avec une de ces directions, sa polarisation n'est pas affectée. Souvenez vous aussi que les deux directions sont perpendiculaires.

• Placez la lame telle que $\vec{E}(t, z = 0)$ est à 45$^\circ$ par rapport aux deux directions principales. Avec l'aide du second polariseur (l'analyseur), cherchez la polarisation résultante.

  • Pour une lame demi onde, nous trouverons que la nouvelle polarisation est symétrique par rapport à l'originale.
  • Pour une lame quart d'onde, nous ne pourrons pas trouver la nouvelle polarisation comme c'est circulaire.

• Identifiez au moins une lame de chaque sorte.

Question: Que se passerait il si nous placions 2 lames quart d'ondes consécutives?

Partie qualitative. Observez divers matériauz anisotropes, en particulier du verre trempé, du cellophane étiré, etc. entre polariseurs. Décrivez les effects obtenus.

Polarisation circulaire, pouvoir rotatoire.

Placez entre polariseurs croisés un tube contenant une solution de sucre. Mesurez la rotation du plan de polarisation.

Question: Si l'angle measuré est $\alpha$, comme on peut être sur que l'angle est vraiment $\alpha$ et non 340$^{\circ}$ - $\alpha$. Comment pourrait-on résoudre cette ambiguité?

Paramètres de Stokes

• Lire la documentation disponible dans le site web du cours sur les paramètres de Stokes.
• Mesurer les paramètres de Stokes d'une/plusieurs sources ayant des polarisations différents.

---

Revision J.A. Aguilar 2015

S. Massar et JM Frère 2007