Gamma-ray Astronomy¶
As we saw, the origin of CR remains a mystery due to the deflection of CRs in their travel. Only CR astronomy at $10^{19}$ eV will be possible, but the GZK limits the horizon.
Gamma-ray astronomy provides an fundamental tool to observe the Universe using neutral deep penetrating gamma-ray particles.
Gamma-rays and X-rays¶
- Originally the distinction between gamma-rays and X-rays was due to the nuclear production mechanism. X-rays are the product of transition of electrons in the atomic shell, while gamma-rays are produced in the atomic nucleus. This distinction also leads to a classification in energy. X-rays are typically below 100 keV. Photons with E > 100 keV are called gamma-rays.
Gamma-ray production mechanism¶
Sources of CR can also produce gamma-rays by different mechanisms roughly divided in two main categories:
Leptonic model
- Synchrotron radiation.
- Inverse Compton Scattering.
Hadronic model
- $\pi^0$ decay.
- Proton synchrotron radiation.
- Others
- Matter-antimatter annihilation, dark matter annihilation and nuclear transformation.
Leptonic models¶
Synchrotron radiation¶
Deflection of charged particles in a magnetic field gives rise to an acceleration motion. An accelerated electrical charge radiates electromagnetic waves.
The power $P$ of emitted synchrotron radiation by a particle of mass $m$ and charge $e$ and momentum $p_\perp$ perpendicular to the magnetic field is, in the classical limit.
$$P_{cl} = \frac{2\alpha}{3m^4}(p_\perp eB)^2$$The energy loss $dE/dt = -P \propto m^{-4}$ and hence is most severe for lightest charged particles, the electrons. The length-scale of electrons is:
$$l_{syn} = \left(\frac{1}{E}\frac{{\rm d}E}{{\rm d}t}\right)^{-1} \sim 100 {\rm \;pc}$$That's why electrons are not the main component of CR. On the other side, they synchrotron radiation of relativistic electrons explains the strong radio emission of many AGNs and typically explains the first peak visible in the spectral energy distribution (SED) of AGNs.
The spectrum of synchrotron radiation generated by a power law spectrum of primary charge particles also follows a power law.
When the charge particle interacts with the Coulomb field of a charge (eg atomic nucleus or electrons) the radiation is called bremsstrahlung.
Leptonic models¶
Inverse Compton scattering.¶
Compton discovered that photons can transfer part of their energy to electrons in a collision. In astrophysics the inverse Compton effect electrons accelerated to high energy collide with photons from the blackbody radiation (thermal photons) or starlight photons and transfer energy to them.
In astrophysics the inverse compton scattering is very important as a fast electrons hitting a low-energy photon transfers a large fraction of its energy to the photon.
The second peak seen in some AGNs is normally due to inverse compton scattering.
Note: In some cases the synchrotron spectrum can interact with the same electron population that generated them via IC, this scenario is called Synchrotron Self Compton (SSC). When external photons are present IC does not need the synchrotron field. Such process is referred as External Inverse Compton (EC) scattering.
AGNs¶
Spectral energy distributions¶
As we saw, blazars are a particular classification of AGNs with their relativistic plasma jet oriented close to the line of sight. These objects exhibit rapid variability and have broadband spectral energy distributions (SEDs) characterized, in a $\nu F_\nu$ representation, by a synchrotron component extending from radio to X-ray frequencies, and a second component peaking at gamma-ray frequencies due to either inverse-Compton radiation (or from hadronic processes).
Spectral energy distribution of nearby (z = 0.044) blazar 1ES 2344+514 during a flaring and a quiet stateAGNs¶
Lightcurves and flares¶
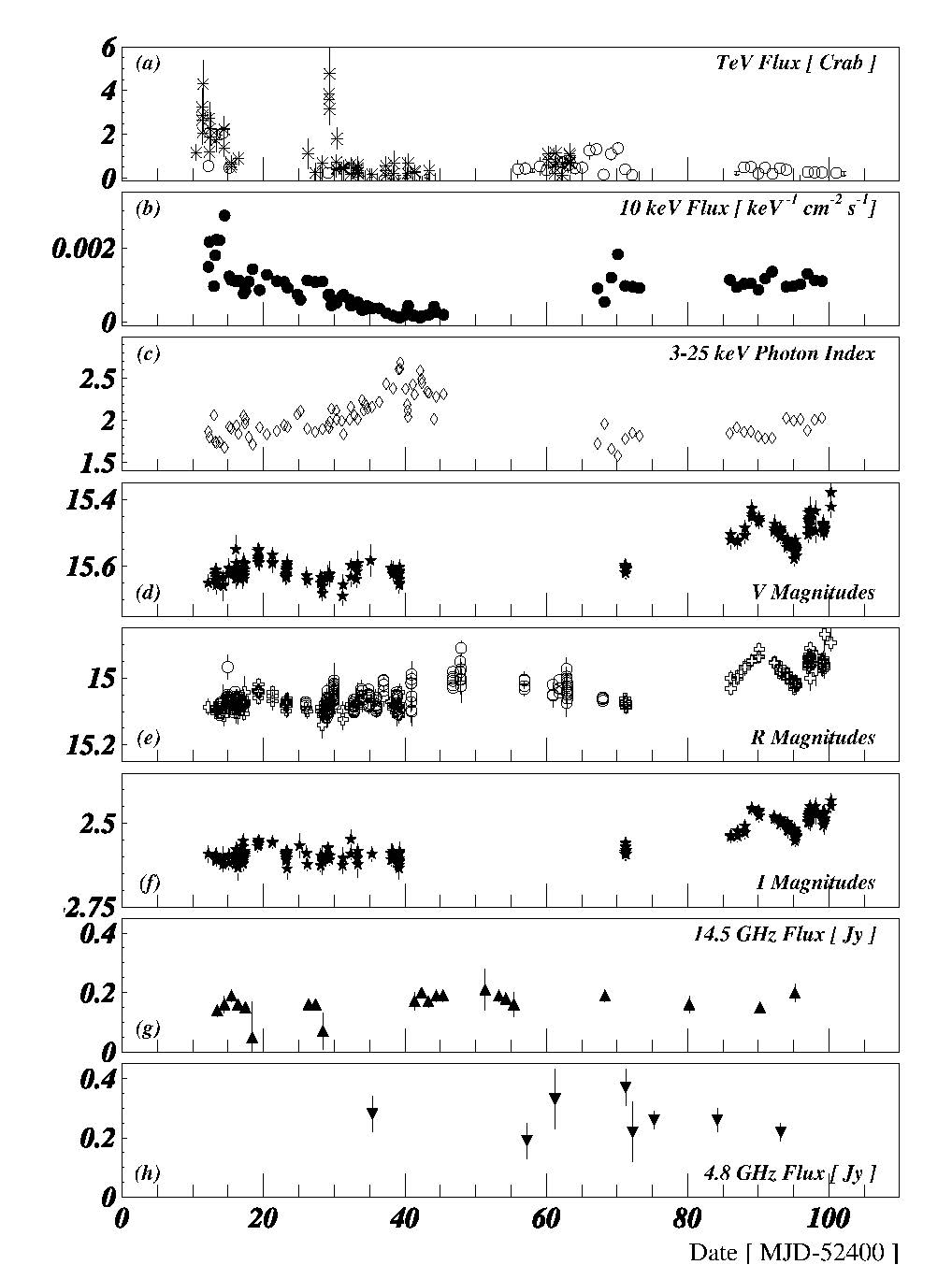
Hadronic models¶
Pion decay¶
Accelerated protons in the source can produce charged and neutral pions. Neutral pions decay rapidly ($\tau = 8.4 \times 10^{-17}$ ns, compared to 26 ns of charged pions) in to two photons. In the CMS each photon from the pion decay has an energy of $E^{*}_\gamma = m_{\pi^0}/2 \approx 70$ MeV as we saw for the 2-body decay. In order to calculate the energy in the lab system we need to make a lorentz transformation:
$$E = \gamma(E^{*} + \beta p^{*} \cos\theta^{*})$$where ($*$) denotes the CMS. Since pion is an isoscalar the decay is isotropic the limits are determined by $\cos\theta^{*} = \pm 1$. These limits are:
$$\frac{m_{\pi^0}}{2}\sqrt{\frac{1-\beta}{1+\beta}} \leq E_\gamma \leq \frac{m_{\pi^0}}{2}\sqrt{\frac{1+\beta}{1-\beta}}$$where $\beta$ is the velocity of the parent pion and we used $p^* = E^*$ for photons.
Hadronic models¶
Pion bump¶
But what is the distribution of photons? Since the decay is isotropic in the CMS:
$${\rm d} N = \frac{1}{4\pi} d\Omega = \frac{1}{2} {\rm d}\cos\theta^*$$Using the lorentz transformation from CMS system and the lab system we can express: ${\rm d}\cos\theta^* = {\rm d}E/\beta p^* = 2{\rm d} E/m_{\pi^0}$ and thus:
$${\rm d} N = \frac{{\rm d} E}{\gamma m_{\pi^0}}$$Then the distribution of photons ${\rm d}N/{\rm d}E = \rm{\; const.}$ ie is constant on a box from $E_{min}$ to $E_{max}$ when plotted as $\log(E_\gamma)$. If many pions are decaying, the distribution of photons will be superpossition of boxes around $m_{\pi^0}$. This is the so-called pion bump.
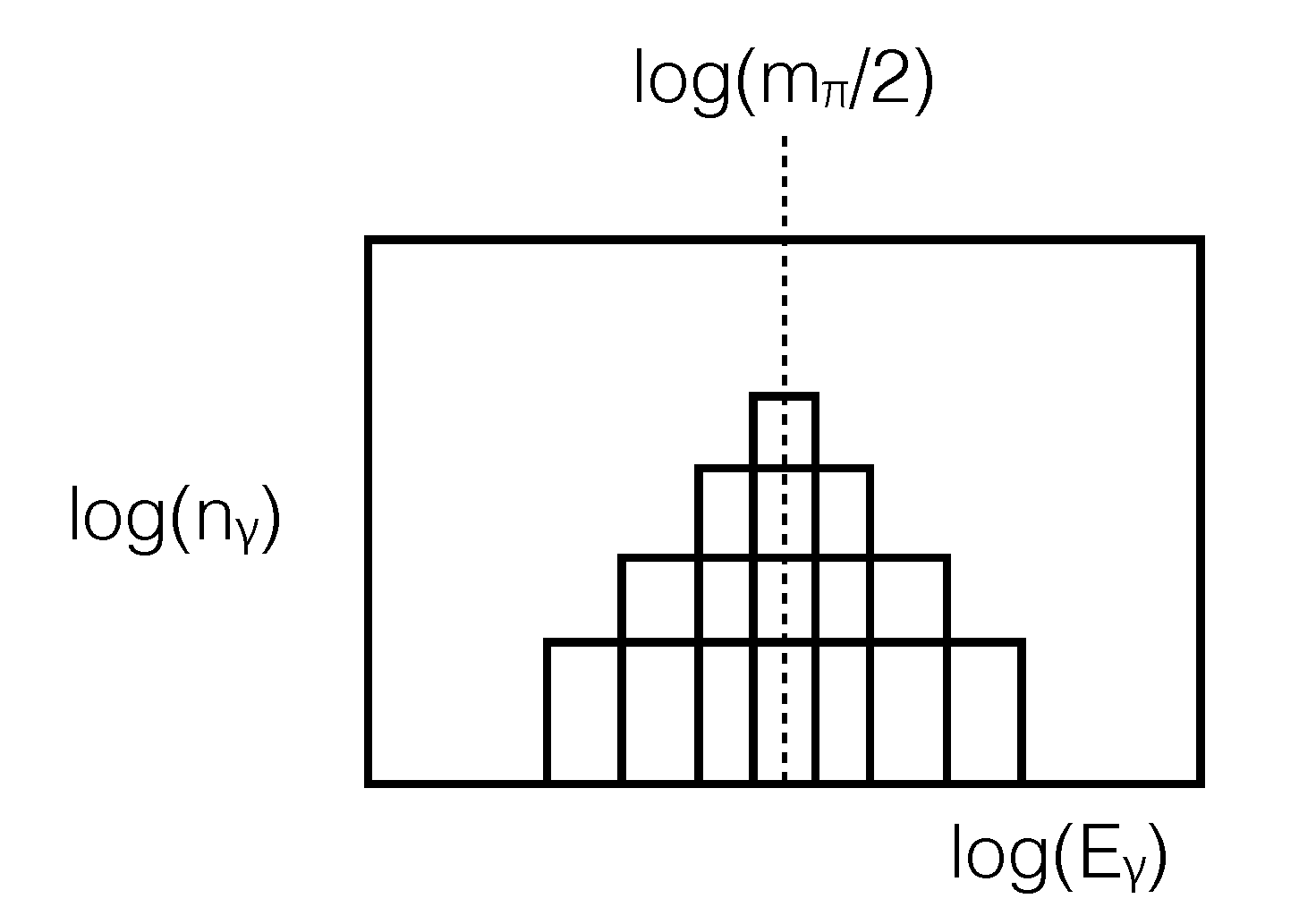
Hadronic models¶
Pion bump in SNR with Molecular Cloud¶
In 2013 Fermi (a gamma-ray satellite) confirmed the pion-bump in two old SNRs with Molecular Cloud.
So did we find the sources of Galactic Cosmic Rays? No. The steep gamma-ray spectrum at high energies suggests that the acceleration is not very active any more (as expected from old SNRs) and hence, even though there might be some particle acceleration these are not the sources of Galactic Cosmic Rays.
Diffuse emission¶
Diffuse gamma-ray emission is that not associated with a particular source. Fermi-LAT observed gamma-ray counts in the energy range from 200 MeV to 100 GeV. The signal is dominated by the diffuse Galactic emission, which is strongest in the plane of our Galaxy and toward the Galactic center but present all over the sky.
Diffuse emission¶
- $\pi^0$-decay (red, long-dashed)
- IC (green, dashed),
- and bremsstrahlung (cyan, dash-dotted).
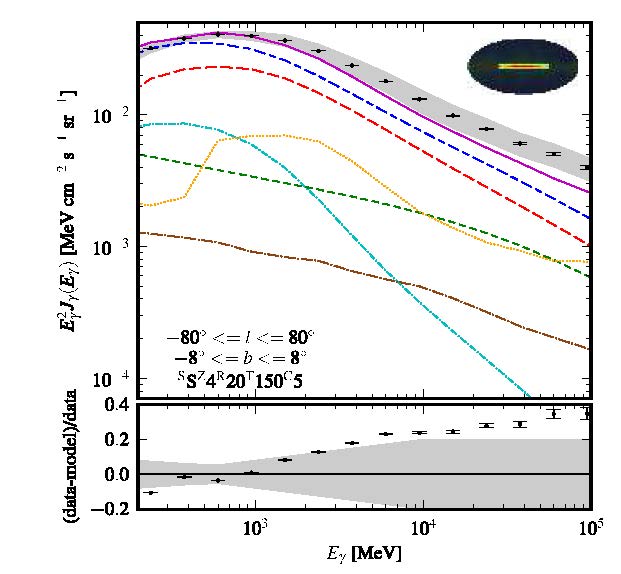Taken from [arXiv:1202.4039](http://arxiv.org/abs/1202.4039)
Extragalactic Background Light¶
As we saw, VHE gamma-rays ($E_\gamma =30$ GeV) have a limited horizon due to their interaction with the CMB and the Extragalactic Background Light (EBL). The TeV signal of distant AGNs are (partially) absorved at the highest energies by the ELB. The absortion is energy dependent and increases with distance. Observations of very far distant AGNs can be used to put constrains on the amount of EBL. However it is difficult tp distinguish between an intrinsic softening of blazar spectra and a softening caused by the interaction with low energy EBL photons.
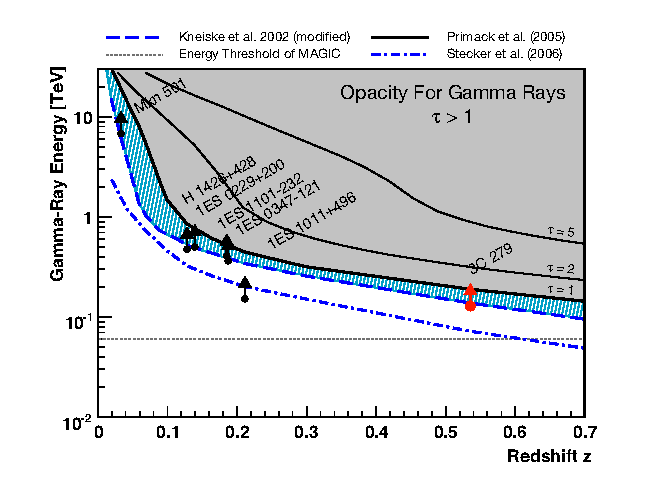Gamma-ray horizon and measurements from some IACTs up to z=0.536. Taken from [arXiv:0904.0774v2](http://arxiv.org/abs/0904.0774)
Gamma-rays, Cosmic-Rays and Neutrinos¶
Both gamma-rays and neutrinos are produced as secondary products of Cosmic-Rays interactions. The dominant channels are:
$$ \begin{align*} p\gamma &\rightarrow \Delta^+ \rightarrow \begin{cases} p \pi^0 & (2/3)\\ n \pi^+ & (1/3) \end{cases}\\ pp &\rightarrow \begin{cases} pp \pi^0 & (2/3)\\ nn \pi^+ & (1/3) \end{cases} \end{align*}$$The same processes occur with neutrons instead of protons leading to $\pi^-$ production. The resulting neutrinos can decay or interact. One assumption is that escaping neutrinos decay as $n \rightarrow p + e^- + \nu_e$ producing the observed CRs. In any case charged and neutral pions will decay as:
$$\begin{align*} \pi^+ &\rightarrow \mu^+ \nu_\mu \rightarrow e^+ \nu_e \bar{\nu}_\mu \nu_\mu\\ \pi^- &\rightarrow \mu^- \bar{\nu}_\mu \rightarrow e^- \bar{\nu}_e \nu_\mu\bar{\nu}_\mu \\ \pi^0 &\rightarrow \gamma\gamma \end{align*}$$Clearly the productions of neutrinos, cosmic-rays and $\gamma$-rays are closely related.
$pp$ interactions¶
The cross section of $pp$ interactions is almost energy independent $\sigma_{pp} \sim 4 \times 10^{-26}$ cm$^2$ (See Kelner et al.). The cross section of this process has a threshold given by:
$$E_{th} = m_p + m_\pi(m_\pi + 4m_p)/2m_p \sim 1.2 {\rm\; GeV}$$Therefore most of accelerated protons can interact in the source and the spectra of secondary particles closely follows that of the parent proton spectrum assuming the meson cooling time (energy loss due to radiation) and interaction length are shorter than decay time/length.
If the proton spectrum is softer than ${\rm d}N_p/{\rm d}E \sim E^{-2}$, most of the electronmagnetic and neutrino power is in the energy band of 1 GeV. Gamma-ray emission is dominated by the $\pi^0$ decay.
If the proton spectrum is harder than ${\rm d}N_p/{\rm d}E \sim E^{-2}$, most of the energy ouput from proton interactions is at high energy. In this case the main contribution in gamma-ray comes from IC from secondary $e^-e^+$ pairs produced in $\pi^{\pm}$ decays.
For environments where radiation density is low (too few photons) $pp$ interactions dominate over $p\gamma$ interactions
$p\gamma$ interations¶
The cross-section of this process has a threshold in higher energies than $pp$ interactions given by:
$$E_{th} = \frac{m_p m_{\pi} + m_{\pi}^2}{\epsilon_{ph}} \simeq 7 \times 10^{16} \left[\frac{\epsilon_{ph}}{1{\rm\; eV}}\right]^{-1}$$where $\epsilon_{ph}$ is the target photon energy. Because this threshold only the highest energy protons can efficiently interact with the soft-photon fields.
Transparent Sources¶
In an accelerator, the target and the beam dump absorbe all the protons and only neutrinos escape. Such beam dumps might exist also in the Universe but they will be hidden sources. So sources might be at least transparent to protons... otherwise we will not see Cosmic Rays!
A generic transparent source can be understood as follows:
Protons are accelerated in a region of high magnetic fields where they interact with photons and generate neutral and charged pions. While the secondary protons may remain trapped in the acceleration region, roughly equal numbers of neutrons and decay products of neutral and charged pions escape. The energy escaping the source is therefore distributed among cosmic rays, gamma rays and neutrinos produced by the decay of neutrons, neutral pions and charged pions.
Waxman-Bahcall flux¶
The neutrino flux from an optical thin (transparent) source is usually referred as the Waxman-Bahcall flux.
Let's assume only the Extragalactic CR. The energy density is, as we calculated in Lecture 3:
$$\rho_{CR} = \int E n(E) {\rm d} E =4\pi \int_{E_{min}}^{E_{max}} \frac{E}{v}I(E) {\rm d} E \sim 3\times 10^{-19} {\rm\; erg\; cm^{-3}}$$where $E_{max}/E_{min} \sim 10^{3}$. We therefore assume that the same energy density ends up in neutrinos and electromagnetic energy. And so:
$$\int E_\nu I_\nu (E_\nu) {\rm d}E_\nu = \frac{\rho_{CR}}{4\pi}$$Assuming that the neutrino follows a power law of spectrum with an differential spectral index of 2 then:
$$E_\nu^2 I_\nu (E_\nu) \sim 5 \times 10^{-8} {\rm \; GeV\; cm^{-2}\; s^{-1}\; sr^{-1}}$$The Waxman-Bahcall flux is sometimes referred as a bound, in part because more energy is transfer to the neutron than the charged pion (roughtly a factor 4 times more) and so:
$$E_{\nu_\mu}^2 I_{\nu_\mu} (E_{\nu_\mu}) \sim 1 - 5 \times 10^{-8} {\rm \; GeV\; cm^{-2}\; s^{-1}\; sr^{-1}}$$In reality the energy density of CR is related with the one of neutrinos as:
$$\rho_{CR}(E_{min}) = x_{\nu/p} \rho_{\nu}(E_{min}) = x_{\nu/p}\int_{E_{min}} n_\nu (E_\nu) E_\nu {\rm d} E_\nu $$where $x_{\nu/p}$ depends on the optical thickness of the $p\gamma$ interactions and on the fraction of energy going to the neutrino. Ignoring the integrals we get the relation:
$$E_\nu I_\nu (E_\nu) \sim n_{\nu/p} E_p I_p (E_p)$$where $n_{\nu/p}$ refers to the number of neutrinos per proton interaction. Using that the energy of the neutrinos will be a fraction $\langle x_{p\rightarrow \nu} \rangle$ of the proton energy we can rewrite it as:
$$I_\nu (E_\nu) \sim n_{\nu/p} \frac{1}{\langle x_{p\rightarrow \nu} \rangle} I_p (E_p)$$The neutrino and gamma connection¶
Extragalactic p$\gamma$¶
Due to isospin the $\Delta^+$ decays more often to $p$ than $n$. $$ p\gamma \rightarrow \Delta^+ \rightarrow \begin{cases} p \pi^0 & (2/3)\ n \pi^+ & (1/3) \end{cases}$$
In both cases, the fraction of energy that goes to the pions is $\langle x_{p\rightarrow\pi}\rangle \sim 0.20$ . Assuming the pion decays:
$$\pi^0 \rightarrow \gamma\gamma, {\rm\;and\;} \pi^+ \rightarrow \mu^+ \nu_\mu \rightarrow e^+ \nu_e \bar{\nu}_\mu \nu_\mu$$We have that:
- $\gamma$'s take 1/2 of the neutral pion energy.
- Leptons take 1/4 of the charge pion energy.
And so:
$$\begin{align*} \langle x_{p\rightarrow\nu}\rangle &= \frac{1}{4}\langle x_{p\rightarrow\pi}\rangle =\frac{1}{20}\\ \langle x_{p\rightarrow\gamma}\rangle &= \frac{1}{2}\langle x_{p\rightarrow\pi}\rangle =\frac{1}{10} \end{align*}$$The value derived before does not account for several things:
- There are more CR than observed at Earth due to the GZK-effect. It also ignores the evolution as red-shift $\rightarrow$ increase the neutrino flux.
- In $p\gamma$ muon neutrinos (and antineutrinos) from the pion decay $\pi^+ \rightarrow \mu^+ \nu_\mu \rightarrow e^+ \nu_e \bar{\nu}_\mu \nu_\mu$ only receive 1/2 of the energy of the charged pion (assuming each lepton carries the same energy) $\rightarrow$ decrease the neutrino flux.
In practice ther corrections compensate. The other uncertainty is from where to chose $E_{min}$ ie the transition to Galactic sources.
The neutrino and gamma connection¶
Extragalactic p$\gamma$¶
If we consider only $\nu_\mu$ we have 2 $\nu_\mu$ per pion decay, as well as 2 $\gamma$'s per pion decay. So the spectra can be related as:
$$\begin{align*} I_{\nu_\mu}(E_{\nu_\mu}) &= 2 \times \frac{1}{3} \frac{1}{\langle x_{p\rightarrow\nu}\rangle} I_{p}(E_{p})\\ I_{\gamma}(E_{\gamma}) &= 2\times \frac{2}{3} \frac{1}{\langle x_{p\rightarrow\gamma}\rangle}I_{p}(E_{p}) \end{align*}$$Let's assume a proton spectrum $I_p(E_p) \propto E_p^{-2}$ and so $I_p(E_p)\propto E_{\nu_\mu}^{-2}\langle x_{p\rightarrow\nu}\rangle^2$
$$\begin{align*} I_{\nu_\mu}(E_{\nu_\mu}) \propto 2 \times \frac{1}{3} \langle x_{p\rightarrow\nu}\rangle E_{\nu_\mu}^{-2} \rightarrow 2 \times \frac{1}{3} \times \frac{1}{20} E_{\nu_\mu}^{-2}\\ I_\gamma(E_\gamma) \propto 2 \times \frac{2}{3}\langle x_{p\rightarrow\gamma}\rangle E_\gamma^{-2} \rightarrow 2 \times \frac{2}{3} \times \frac{1}{10} E_{\gamma}^{-2} \end{align*}$$So:
$$I_{\nu_\mu} (E_{\nu_\mu}) \sim \frac{1}{4} I_{\gamma}(E_\gamma)$$The neutrino and gamma connection¶
Galactic $pp$¶
In Galactic SN shocks CRs interact with the H in the Galactic disk (pp interactions, lower threshold than $p\gamma$. Let's consider the reaction:
$$pp \rightarrow p p \pi^0 + \pi^+ \pi^-$$where the pions take each 1/3 of the energy. Doing the same calculation as before we get that:
$$\begin{align*} I_{\nu_\mu}(E_{\nu_\mu}) &\propto 2 \times \frac{1}{3} \langle x_{p\rightarrow\nu}\rangle E_{\nu_\mu}^{-2} \rightarrow 2 \times \frac{2}{3} \times \frac{1}{20} E_{\nu_\mu}^{-2}\\ I_\gamma(E_\gamma) &\propto 2 \times \frac{2}{3}\langle x_{p\rightarrow\gamma}\rangle E_\gamma^{-2} \rightarrow 2 \times \frac{1}{3} \times \frac{1}{10} E_{\gamma}^{-2} \end{align*}$$Astrophysical Neutrino Oscillations¶
We saw that the probability of neutrino flavor for $\delta = 0$ can be written as:
$$\begin{align*} P(\nu_\alpha \rightarrow \nu_\beta) &=\sum_j\sum_i U_{\alpha i}U^*_{\beta i}U^*_{\alpha j}U_{\beta j}e^{-i\frac{\Delta m^2L}{2E}}\\ &= \delta_{\alpha\beta} - 4{\sum_{i>j}{\rm Re}(U_{\alpha i}^{*}U_{\beta i}U_{\alpha j}U_{\beta j}^{*}})\sin^{2}(\frac{\Delta m_{ij}^{2}L}{4E}) \end{align*}$$For a non-monochromatic neutrino beam, the probability has to be averaged over the spectrum. The $\sin$ term will be averaged to 0.5 for large distances $L$. And thus the probability does not depend on time and can be written as a matrix:
$$P(\nu_\alpha \rightarrow \nu_\beta) = \sum_j |U_{\alpha j}|^2 |U_{\beta j}|^2 $$Calculation of astrophysical neutrino oscillations¶
import numpy as np
import scipy as sp
def PMNS_Factory(t12, t13, t23, d):
s12 = np.sin(t12)
c12 = np.cos(t12)
s23 = np.sin(t23)
c23 = np.cos(t23)
s13 = np.sin(t13)
c13 = np.cos(t13)
cp = np.exp(1j*d)
return np.array([[ c12*c13, s12*c13, s13*np.conj(cp) ],
[-s12*c23 - c12*s23*s13*cp, c12*c23 - s12*s23*s13*cp, s23*c13],
[ s12*s23 - c12*s23*s13*cp,-c12*s23 - s12*c23*s13*cp, c23*c13]])
##Probability of flavor change when L->inf
def Prob(a, b, U):
"""
Gives the oscillation probability for nu(a) -> nu(b)
for PMNS matrix U, and L in km and E in GeV
"""
s = 0
for i in range(3):
s += (np.conj(U[a,i])*U[b,i]*U[a,i]*np.conj(U[b,i])).real
return s
def ProbMatrix(U):
return np.array([[Prob(0, 0, U), Prob(0, 1, U), Prob(0,2,U)],
[Prob(1, 0, U), Prob(1, 1, U), Prob(1,2,U)],
[Prob(2, 0, U), Prob(2, 1, U), Prob(2,2,U)]])
t12 = np.arcsin(0.306**0.5)
t13 = np.arcsin(0.0251**0.5)
t23 = np.arcsin(0.42**0.5)
U = PMNS_Factory(t12, t13, t23, 0)
The probability of a ntruno flavor fector of $(\nu^{source}_e, \nu^{source}_\mu, \nu^{source}_\tau)$ to change into a flavor vector $(\nu^{Earth}_e, \nu^{Earth}_\mu, \nu^{Earth}_\tau)$ is given by:
$$\begin{pmatrix}\left.\nu^{Earth}_e \\ \nu^{Earth}_\mu \\ \nu^{Earth}_\tau\right.\end{pmatrix} = P_{\alpha\beta} \begin{pmatrix}\left.\nu^{Source}_e \\ \nu^{Source}_\mu \\ \nu^{Source}_\tau\right.\end{pmatrix} $$Assuming at the source the flavor ratio is (1:2:0) we have that:
source = np.array([1, 2, 0])
P = ProbMatrix(U)
Earth = np.dot(P, source)
print Earth
Thus, almost equal number of eletron, muon and tau astrophysical neutrinos are expected to be observed at Earth due to oscillations. More info at arXiv:hep-ph/0005104
Gamma-ray neutrino relation¶
After oscillations the neutrino and gamma-rays relations are given by:
$$\frac{{\rm d}N_\nu}{{\rm d}E_\nu} = \frac{1}{2}\frac{{\rm d}N_\gamma}{{\rm d}E_p} {\rm\; for\;} p + p$$$$\frac{{\rm d}N_\nu}{{\rm d}E_\nu} = \frac{1}{8}\frac{{\rm d}N_\gamma}{{\rm d}E_p} {\rm\; for\;} p + \gamma$$Assuming an $E^{-2}$ spectrum.
Gamma-ray Astronomy¶
The atmosphere¶
The Earth's atmosphere is opauqe to photons with energy above 10 eV, meaning that to observe gamma-rays directly we need to place the detector above the atmosphere. A turning point in gamma-ray astronomy was the launch of the first satellite-borne telescope, SAS-2, in 1972.
The mayor limitation of satellite experiments is their low area which limits their use to $\leq 100$ GeV. At 100 GeV is when electromagnetic showers from the initial photon can be detected in ground-based telescopes.
Gamma-ray and neutrino detection¶
Most of the gamma-ray and neutrino telescopes make use of the Cherenkov emission to detect the primary $\gamma$-ray and neutrino.
Cherenkov emission.¶
In the relativistic limit $\beta \sim 1$ we can write:
$$\sin \theta = \sqrt{1 - \frac{1}{n^2}} = \sqrt{\frac{n^2 - 1}{n^2}} = \sqrt{\frac{(n-1)(n+1)}{n^2}} \approx \sqrt{2(n-1)}$$%matplotlib inline
import numpy as np
import matplotlib.pylab as plt
import seaborn as sea
from IPython.display import Latex
sea.set_context("poster")
diffn = np.logspace(-4, 0, 100) #n - 1 form 0.0001 to 1
fig, ax = plt.subplots()
#In the relativistic limit
ax.plot(diffn, np.degrees(np.arcsin(np.sqrt(2*diffn))))
ax.set_yscale("log")
ax.set_xscale("log")
ax.set_xlabel("n - 1 ")
ax.set_ylabel(r"$\theta_C$")
plt.show()
#For water n = 1.33
thetaw = np.degrees(np.arcsin(np.sqrt(2*(1.33 -1))))
Latex(r"Cherenkov angle in water: $\theta_C = %.2f^{\circ}$"%thetaw)
#For the atmosphere n = 1.0003
thetaatm = np.degrees(np.arcsin(np.sqrt(2*(1.003 -1))))
Latex(r"Cherenkov angle in the atmosphere: $\theta_C = %.2f^{\circ}$"%thetaatm)
Cherenkov radiation¶
Number of photons¶
The numbe of photons from Cherenkov radiation follows the Frank-Tamn formula:
$$\frac{{\rm d}N}{{\rm d}x} = 2 \pi \alpha z^2\int_{\lambda_1}^{\lambda_2} \sin^2\theta \frac{{\rm d}\lambda}{\lambda^2} $$For relativistic particles, $\beta \sim 1$ in water $n = 1.33$ the Cherenkov spectrum is:
import scipy.constants as cte
alpha = cte.alpha #fine structure constant
fig, ax = plt.subplots()
wl = np.arange(200, 500,1)
n = 1.33
ax.plot(wl, 2 * np.pi * alpha * ( 1- 1/n**2)/wl**2)
ax.set_xlabel("$\lambda$ [nm]")
ax.set_ylabel(r"$\frac{{\rm d}N_\gamma}{{\rm d}x {\rm d}\lambda}}$ (photons nm$^{-2}$)")
plt.show()
Most of the Cherenkov emission goes in to the blue and UV light...
Why there is no X-ray or $\gamma$-ray Cherenkov photons?
Atmospheric extintion.¶
One in the atmosphere, the Cherenkov light can suffer absortion and scattering due to several processes:
- Rayleigh scattering: $$ I = I_0 \frac{8\pi^4 \alpha^2}{\lambda^4 R^2}(1 - \cos^2\theta)$$ where $R$ is the distance to the particle and $\theta$ the scattering angle.
- Absortion by ozone, above 20 km.
- Aerosol, dust. Independent of $\lambda$.
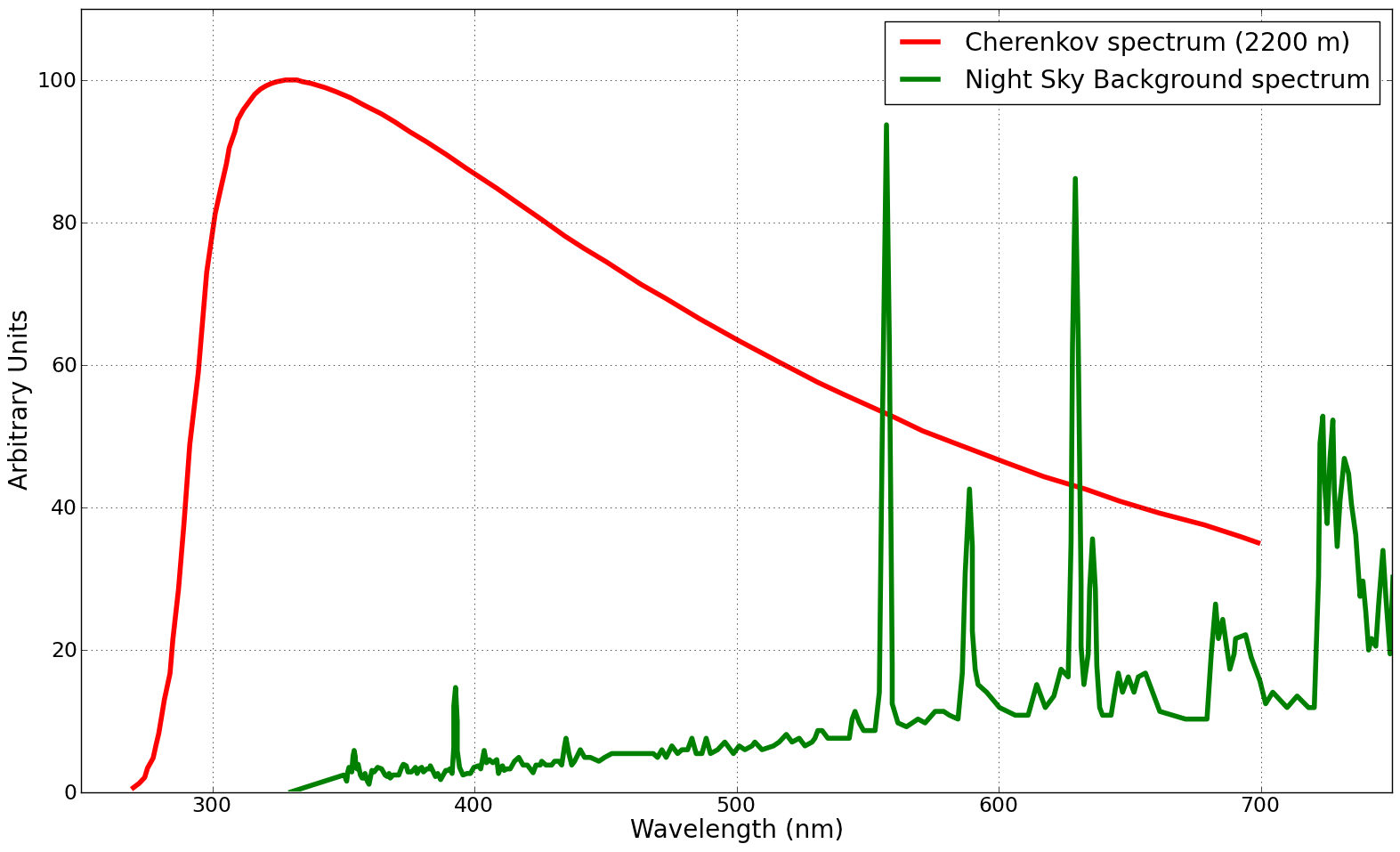
This processes change the Cherenkov spectrum dependending on the altitude. In ice on the other hand, there is no UV absorption and the Cherenkov spectrum keeps the $1/\lambda^2$ tendency.
Next¶
- Detetection technique and $\gamma$-ray and neutrino telescopes.